题目内容
已知x1是方程x＋lg x＝3的一个根，x2是方程x＋10x＝3的一个根，那么x1＋x2的值是
[ ]
A．6
B．3
C．2
D．1
答案：B
解析：
提示：
解析：
|
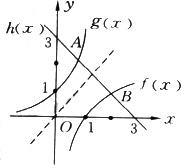
解：将已知的两个方程变形得lg x＝3－x，10x＝3－x． 令f(x)＝lg x，g(x)＝10x，h(x)＝3－x． 如图所示．
记g(x)与h(x)的交点为A(x1，y1)，f(x)与h(x)的交点为B(x2，y2)，利用函数的性质易知A、B两点关于直线y＝x对称，便有x1＝y2，x2＝y1的结论．将A点坐标代入直线方程，得y1＝3－x1，再将y1＝x2代入上式，得x2＝3－x1，即x1＋x2＝3． |
提示：
|
分析：这是一个研究方程的根的问题，如果采用纯代数的方法，从解方程或方程组的方法入手，将很困难，有些问题甚至无法解决．于是我们想到构造函数，利用函数图象，借助数形结合的思想来解决． 评注：此类题一般采用构造函数，应用数形结合求解．需指出，我们仅能求解一些特殊的此类问题，对于一般的问题，在目前阶段没有普遍的方法求解．如方程log2x＝x2－2，2x2＋2x＝3，a|x|＝|logax|等等，这类问题的解均无普遍方法求得．我们只能借助数形结合得到方程解的个数或解的大致范围．因此，此类问题一般都是研究解的个数和解的范围． |
练习册系列答案
相关题目
时，f（x）取得极小值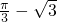
．
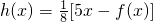，设x1是方程h（x）-x=0的实数根，若对于h（x）定义域中任意的x2、x3，当|x2-x1|＜1，且|x3-x1|＜1时，问是否存在一个最小的正整数M，使得|h（x3）-h（x2）|≤M恒成立，若存在请求出M的值；若不存在请说明理由．
=1上的动点，以M为切点的切线l与直线y=2相交于点P．
，则以Q为切点的椭圆的切线方程是：
．