题目内容
已知:向量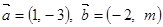 ,且
,且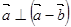 。
。
(1)求实数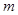 的值;
的值;
(2)当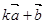 与
与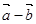 平行时,求实数
平行时,求实数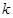 的值。
的值。
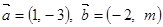 ,且
,且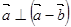 。
。(1)求实数
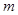 的值;
的值;(2)当
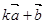 与
与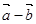 平行时,求实数
平行时,求实数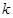 的值。
的值。解:(1) ,……… 3分
,……… 3分
由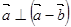 得
得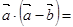 0………5分
0………5分
即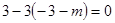 ,故
,故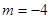 ;………7分
;………7分
(2)由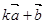
 ,
,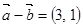
当 平行时,
平行时,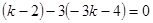 ,
,
从而 。………14分
。………14分
 ,……… 3分
,……… 3分由
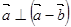 得
得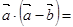 0………5分
0………5分即
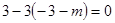 ,故
,故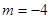 ;………7分
;………7分(2)由
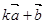
 ,
,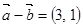
当
 平行时,
平行时,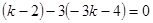 ,
,从而
 。………14分
。………14分本试题主要是考查了向量的共线和向量的数量积知识的综合运用。判定垂直问题等知识点的考查。
(1)第一问中先求解向量的差的坐标,然后利用垂直时,数量积为零得到m的值。
(2)根据向量的共线,得到坐标关系式,从而得到k的值。
(1)第一问中先求解向量的差的坐标,然后利用垂直时,数量积为零得到m的值。
(2)根据向量的共线,得到坐标关系式,从而得到k的值。

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 与圆
与圆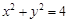 交于
交于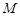 、
、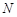 两点,若满足
两点,若满足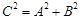 ,则
,则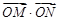 (
(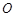 为坐标原点)等于( ).
为坐标原点)等于( ).
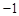

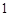
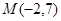 ,
,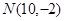 ,点
,点 是线段
是线段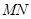 上的点,且
上的点,且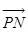
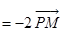 ,则
,则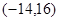
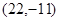
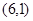
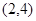
 ,它们所对应的点分别为A,B,C.若
,它们所对应的点分别为A,B,C.若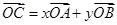 ,则
,则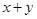 的值是 .
的值是 .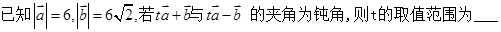
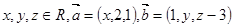 ,且
,且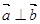 ,则
,则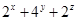 的最小值是( )
的最小值是( )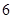
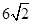
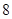
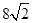
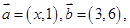
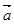 ∥
∥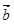 ,则实数
,则实数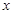 的值为( )
的值为( )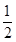
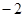
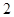
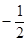
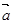 =(3,1),
=(3,1),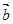 =(
=(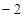 ,5)则3
,5)则3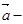 2
2 )
)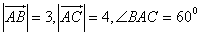 ,则
,则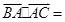 ( )
( )