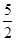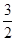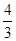题目内容
下图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为 和
和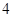 ,腰长为
,腰长为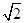 的等腰梯形, 则该几何体的体积是
的等腰梯形, 则该几何体的体积是
A.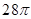 | B. | C. | D. |
C
解析试题分析:解:正视图和侧视图都是一个两底长分别为2和4,腰长为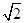 的等腰梯形,俯视图是两个圆中间的圆是虚线,∴几何体是一个圆台,圆台的上底是一个直径为2,下底的直径为4,母线长是
的等腰梯形,俯视图是两个圆中间的圆是虚线,∴几何体是一个圆台,圆台的上底是一个直径为2,下底的直径为4,母线长是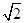 的圆台,圆台的高是
的圆台,圆台的高是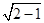 =1,∴圆台的体积是
=1,∴圆台的体积是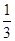 (π+
(π+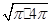 +4π)×1=
+4π)×1= 故选C.
故选C.
考点:三视图确定几何图形
点评:本题考查由三视图确定几何图形,根据条件中所给的数据求几何体的体积,考查圆台的体积公式,本题是一个基础题

练习册系列答案
相关题目
一个空间几何体的三视图如右图所示,则该几何体的外接球的表面积为( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则它的体积是( )
A. | B.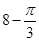 |
C. | D. |
如图,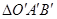 是
是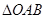 水平放置的直观图,则
水平放置的直观图,则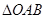 的面积为( )
的面积为( )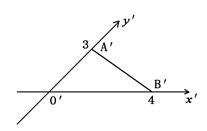
| A.12 | B.6 | C.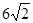 | D.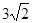 |
一个几何体的三视图如图所示,则该几何体的体积为( )
| A.1 | B. |
C. | D. |
在下列命题中,不是公理的是( )
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 |