题目内容
已知f(x)=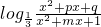 .是否存在实数p、q、m,使f(x)同时满足下列三个条件:
.是否存在实数p、q、m,使f(x)同时满足下列三个条件:
①定义域为R的奇函数;
②在[1,+∞)上是减函数;
③最小值是-1.若存在,求出p、q、m;若不存在,说明理由.
解:∵f(x)是定义域为R的奇函数,
∴f(0)=0 即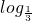 q=0,得q=1
q=0,得q=1
又f(-x)=-f(x)
∴ =-
=-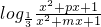 ,
,
∴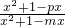 =
=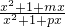 ,
,
即(x2+1)2-p2x2=(x2+1)2-m2x2
∴p2=m2
若p=m,则f(x)=0,不合题意.故p=-m≠0
∴f(x)=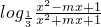
由f(x)在[1,+∞)上是减函数,
x≠0时,令g(x)=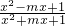 =1-
=1-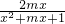 =1-
=1-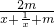
∵ 在[1,+∞)上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减.
在[1,+∞)上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减.
即m>0时函数f(x)在(-∞,-1)上为减函数,在(-1,0)上为增函数,在(0,1)上为增函数,在(1,+∞)上为减函数
∴x=-1时, 在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.
在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.
∴1-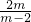 =3 得m=1,从而p=-1
=3 得m=1,从而p=-1
综上可知,存在p=-1,q=1,m=1.
分析:先利用奇函数的定义得q=1,且p=-m≠0,再利用复合函数法,结合已知函数的单调区间判断m>0,从而确定函数f(x)的单调区间,最后结合单调性与已知的最小值,推测只能当x=-1时函数f(x)取最小值-1,从而解得m的值,进而得p、q、m的值
点评:本题考查了奇函数的定义及其应用,复合函数法判断函数的单调性,并利用单调性求函数最值的方法,逻辑推理能力和运算能力
∴f(0)=0 即
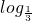 q=0,得q=1
q=0,得q=1又f(-x)=-f(x)
∴
 =-
=-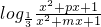 ,
,∴
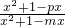 =
=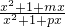 ,
,即(x2+1)2-p2x2=(x2+1)2-m2x2
∴p2=m2
若p=m,则f(x)=0,不合题意.故p=-m≠0
∴f(x)=
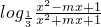
由f(x)在[1,+∞)上是减函数,
x≠0时,令g(x)=
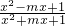 =1-
=1-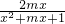 =1-
=1-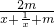
∵
 在[1,+∞)上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减.
在[1,+∞)上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞)上g(x)递增,从而f(x)递减.即m>0时函数f(x)在(-∞,-1)上为减函数,在(-1,0)上为增函数,在(0,1)上为增函数,在(1,+∞)上为减函数
∴x=-1时,
 在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.
在(-∞,-1]上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.∴1-
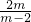 =3 得m=1,从而p=-1
=3 得m=1,从而p=-1综上可知,存在p=-1,q=1,m=1.
分析:先利用奇函数的定义得q=1,且p=-m≠0,再利用复合函数法,结合已知函数的单调区间判断m>0,从而确定函数f(x)的单调区间,最后结合单调性与已知的最小值,推测只能当x=-1时函数f(x)取最小值-1,从而解得m的值,进而得p、q、m的值
点评:本题考查了奇函数的定义及其应用,复合函数法判断函数的单调性,并利用单调性求函数最值的方法,逻辑推理能力和运算能力

练习册系列答案
相关题目