题目内容
已知椭圆 +
+ =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于 ,抛物线x2=2py (p>0).
,抛物线x2=2py (p>0).
(1)若抛物线的焦点F在椭圆的顶点上,求椭圆和抛物线的方程;
(2)若抛物线的焦点F为(0, ),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)由椭圆方程得:a=2,e= =
=
∴c= ,∴
,∴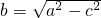 =1
=1
∴椭圆方程为 ;
;
由题意得:抛物线的焦点应为椭圆的上顶点,即(0,1)点,∴p=2
∴抛物线方程为x2=4y
(2)由题意可得p=1,∴抛物线方程为x2=2y…①
设抛物线上存在一点P(a,b),则抛物线在点P处的切线斜率为k=y′|x=a=a
∴过点P的切线方程为y-b=a(x-a),即y=ax-b
代入椭圆方程,可得(4a2+1)x2-8abx+4b2-4=0…②
设切线与椭圆的交点A(x1,y1),B(x2,y2),故x1+x2=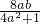 ,x1x2=
,x1x2=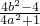
∴ =x1x2+y1y2═
=x1x2+y1y2═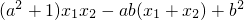 =
=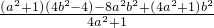
∵OA⊥OB,∴ =0
=0
∴4a2-5b2+4=0
代入a2=2b可得5b2-8b-4=0
∴b=2或- (舍去)
(舍去)
b=2代入①得a=±2
将a,b代入②检验△=208>0
∴存在这样的点P(±2,2)满足条件.
分析:(1)利用椭圆的几何性质,确定椭圆的方程,可得抛物线的焦点,即可求抛物线的方程;
(2)求出过P的切线方程,代入椭圆方程,利用韦达定理及向量的数量积公式,即可求得结论.
点评:本题考查椭圆、抛物线的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
 =
=
∴c=
 ,∴
,∴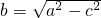 =1
=1 ∴椭圆方程为
 ;
;由题意得:抛物线的焦点应为椭圆的上顶点,即(0,1)点,∴p=2
∴抛物线方程为x2=4y
(2)由题意可得p=1,∴抛物线方程为x2=2y…①
设抛物线上存在一点P(a,b),则抛物线在点P处的切线斜率为k=y′|x=a=a
∴过点P的切线方程为y-b=a(x-a),即y=ax-b
代入椭圆方程,可得(4a2+1)x2-8abx+4b2-4=0…②
设切线与椭圆的交点A(x1,y1),B(x2,y2),故x1+x2=
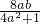 ,x1x2=
,x1x2=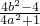
∴
 =x1x2+y1y2═
=x1x2+y1y2═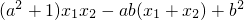 =
=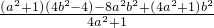
∵OA⊥OB,∴
 =0
=0∴4a2-5b2+4=0
代入a2=2b可得5b2-8b-4=0
∴b=2或-
 (舍去)
(舍去)b=2代入①得a=±2
将a,b代入②检验△=208>0
∴存在这样的点P(±2,2)满足条件.
分析:(1)利用椭圆的几何性质,确定椭圆的方程,可得抛物线的焦点,即可求抛物线的方程;
(2)求出过P的切线方程,代入椭圆方程,利用韦达定理及向量的数量积公式,即可求得结论.
点评:本题考查椭圆、抛物线的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
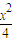 +
+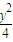 =1(0<b<2)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C作圆P.
=1(0<b<2)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C作圆P.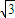 时,求圆P的方程;
时,求圆P的方程; =1(0<b<5)的离心率为
=1(0<b<5)的离心率为 ,则b等于( )
,则b等于( ) +
+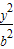 =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于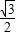 ,抛物线x2=2py (p>0).
,抛物线x2=2py (p>0). ),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.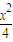 +
+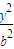 =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于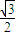 ,抛物线x2=2py (p>0).
,抛物线x2=2py (p>0). ),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足OA⊥OB?若存在,求出点P的坐标;若不存在,请说明理由.