题目内容
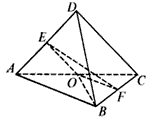
把正方形ABCD沿其对角线AC折成直二面角D-AC-B后,连接BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点。

(1)求证:AB∥平面EOF;
(2)求二面角E-OF-B的大小。
(2)求二面角E-OF-B的大小。
解:(1)∵点O、F分别为线段AC、BC的中点,
∴OF∥AB
∵OF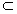 平面EOF,AB
平面EOF,AB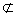 平面EOF
平面EOF
∴AB∥平面EOF。
∴OF∥AB
∵OF
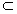 平面EOF,AB
平面EOF,AB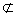 平面EOF
平面EOF∴AB∥平面EOF。
(2)∵二面角D-AC-B为直二面角,连接OD
∵AD=DC
∴OD⊥AC
∵平面ADC⊥平面ABC,
∴OD⊥平面ABC
又AB=BC
∴OB⊥AC
于是可建立如图所示的空间直角坐标系O-xyz
由题可设OA=OB=OC=OD=2a,
∵点E、F分别为线段AD、BC的中点,
∴A(0,- 2a,0),B(2a,0,0),C(0,2a,0),D(0,0,2a), E(0,-a,a),F(a,a,0)
∴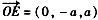 ,
,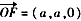
设平面EOF的一个法向量为n1=(x,y,z)
由 得
得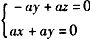
取x=-1
则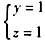
∴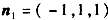
设平面OBF的一个法向量为n2=(0,0,1)
∵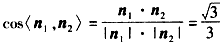
∴二面角E-OF-B的大小为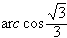 。
。
∵AD=DC
∴OD⊥AC
∵平面ADC⊥平面ABC,
∴OD⊥平面ABC
又AB=BC
∴OB⊥AC
于是可建立如图所示的空间直角坐标系O-xyz
由题可设OA=OB=OC=OD=2a,
∵点E、F分别为线段AD、BC的中点,
∴A(0,- 2a,0),B(2a,0,0),C(0,2a,0),D(0,0,2a), E(0,-a,a),F(a,a,0)
∴
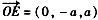 ,
,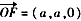
设平面EOF的一个法向量为n1=(x,y,z)
由
 得
得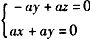
取x=-1
则
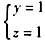
∴
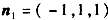
设平面OBF的一个法向量为n2=(0,0,1)
∵
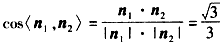
∴二面角E-OF-B的大小为
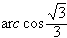 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
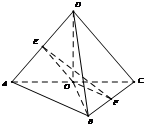 把正方形ABCD沿其对角线AC折成直二面角D-AC-B后,连接BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点.
把正方形ABCD沿其对角线AC折成直二面角D-AC-B后,连接BD,得到如图所示的几何体,已知点O、E、F分别为线段AC、AD、BC的中点.