题目内容
甲、乙两人约定某天晚上7:00~8:00之间在某处会面,并约定甲早到应等乙半小时,而乙早到无需等待即可离去,那么两人能会面的概率是( )
A.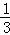 | B.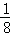 | C.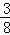 | D.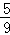 |
C
解析试题分析:设甲到达会面处的时该为7点x分钟,则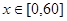 ,设乙到达会面处的时该为7点y分钟,则
,设乙到达会面处的时该为7点y分钟,则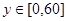 ;根据题意知所有可能情况为不等式组
;根据题意知所有可能情况为不等式组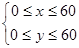 ,两人能会面则必须满足
,两人能会面则必须满足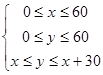 ,画出不等式组所表示的平面区域:
,画出不等式组所表示的平面区域: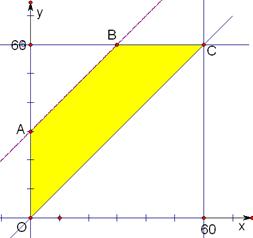 ,则所求的概率为:
,则所求的概率为: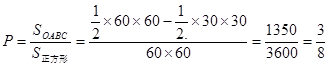 ,故选C.
,故选C.
考点:几何概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(8分)某医院有内科医生12名,外科医生8名,现要派5名医生参加赈灾医疗队,则:
(1)某内科医生必须参加,某外科医生不能参加,有多少种选法?
(2)至少有一名内科医生且至少有一名外科医生参加有几种选法?
给出如下四对事件:①某人射击1次,“射中7环”与“射中8环”;
②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”;
③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”;
④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”,
其中属于互斥事件的有( )
| A.1对 | B.2对 | C.3对 | D.4对 |
在区间[-3,3]上任取两数x,y,使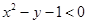 成立的概率为
成立的概率为
A.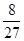 | B.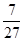 | C. | D.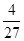 |
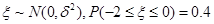 ,则
,则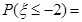 ( )
( )
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
如果随机变量X~N(2,22),若P(X<a)=0.2,则P(X<4-a)=( )
| A.0.2 | B.0.4 | C.0.6 | D.0.8 |
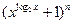 的展开式中第6项与第7项的系数之比为2:3,求n;若展开式的倒数第二项为112,求
的展开式中第6项与第7项的系数之比为2:3,求n;若展开式的倒数第二项为112,求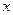 的值。(12分)
的值。(12分)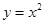 图象下方的点构成的区域(阴影部分).向D中随机投一点,则该点落入E中的概率为
图象下方的点构成的区域(阴影部分).向D中随机投一点,则该点落入E中的概率为



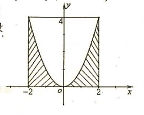
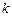 ,
,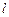 是给定的两个正整数.证明:有无穷多个正整数
是给定的两个正整数.证明:有无穷多个正整数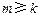 ,使得
,使得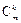 与
与