题目内容
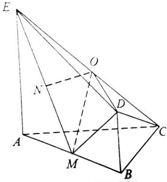 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=| 1 | 2 |
(1)求证:OD∥平面ABC;
(2)求证:ON⊥平面ABDE;
(3)求直线CD与平面ODM所成角的正弦值.
分析:(1)利用三角形的中位线的性质,先证明四边形ODBF是平行四边形,从而可得OD∥FB,利用线面平行的判定,可以证明OD∥平面ABC;
(2)利用平面ABDE⊥平面ABC,证明BD⊥平面ABC,进而可证ON⊥平面ABDE;
(3)建立空间直角坐标系,确定平面ODM的法向量
=(-3,1,
),利用向量的夹角公式,可求直线CD与平面ODM所成角的正弦值.
(2)利用平面ABDE⊥平面ABC,证明BD⊥平面ABC,进而可证ON⊥平面ABDE;
(3)建立空间直角坐标系,确定平面ODM的法向量
| n |
| 2 |
解答:(1)证明:如图1,取AC中点F,连接OF,BF.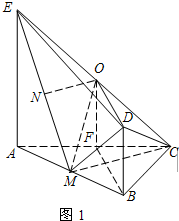
∵O是EC中点,∴OF是△CAE的中位线,∴OF∥EA,且OF=
EA,
又DB∥EA,且DB=
EA,∴OF∥DB且OF=DB,∴四边形ODBF是平行四边形,
∴OD∥FB.
∵OD?面ABC,FB?面ABC,OD∥平面ABC.…(5分)
(2)证明:连接CM,
∵N是EM的中点,∴ON∥CM.
∵平面ABDE⊥平面ABC,平面ABDE∩平面ABC=AB,BD?平面ABDE,BD⊥AB,
∴BD⊥平面ABC,
∵CM?平面ABC,∴BD⊥CM,∴BD⊥ON.
又△ABC是等腰直角三角形,AC=BC,M是AB的中点,∴CM⊥AB,∴ON⊥AB,
由AB,DB?平面ABDE,AB∩DB=B,∴ON⊥平面ABDE.…(11分)
(3)解:建立如图2所示的空间直角坐标系.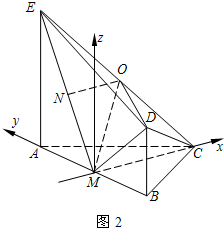
由条件,得M(0,0,0),C(2
,0,0),E(0,2
,4),D(0,-2
,2),O(
,
,2),
∴
=(
,
,2),
=(0,-2
,2),
=(-2
,-2
,2),
设平面ODM的法向量为
=(x,y,z),
由
⊥
,
⊥
,
∴
,取
=(-3,1,
),
设直线CD与平面ODM所成角为θ,则sinθ=|cos?
>|=|
|=
,
∴直线CD与平面ODM所成角的正弦值为
. …(16分)

∵O是EC中点,∴OF是△CAE的中位线,∴OF∥EA,且OF=
| 1 |
| 2 |
又DB∥EA,且DB=
| 1 |
| 2 |
∴OD∥FB.
∵OD?面ABC,FB?面ABC,OD∥平面ABC.…(5分)
(2)证明:连接CM,
∵N是EM的中点,∴ON∥CM.
∵平面ABDE⊥平面ABC,平面ABDE∩平面ABC=AB,BD?平面ABDE,BD⊥AB,
∴BD⊥平面ABC,
∵CM?平面ABC,∴BD⊥CM,∴BD⊥ON.
又△ABC是等腰直角三角形,AC=BC,M是AB的中点,∴CM⊥AB,∴ON⊥AB,
由AB,DB?平面ABDE,AB∩DB=B,∴ON⊥平面ABDE.…(11分)
(3)解:建立如图2所示的空间直角坐标系.

由条件,得M(0,0,0),C(2
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴
| MO |
| 2 |
| 2 |
| MD |
| 2 |
| CD |
| 2 |
| 2 |
设平面ODM的法向量为
| n |
由
| n |
| MO |
| n |
| MD |
∴
|
| n |
| 2 |
设直线CD与平面ODM所成角为θ,则sinθ=|cos?
| n, |
| CD |
6
| ||||||
2
|
| ||
| 10 |
∴直线CD与平面ODM所成角的正弦值为
| ||
| 10 |
点评:本题考查线面平行,考查线面垂直,考查线面角,解题的关键是正确运用线面平行与垂直的判定与性质,正确运用向量法求线面角.

练习册系列答案
相关题目
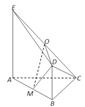 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,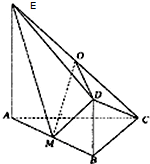 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA, 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=