题目内容
命题 关于
关于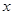 的不等式
的不等式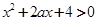 对一切
对一切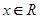 恒成立;命题
恒成立;命题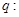 函数
函数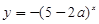 是减函数,若
是减函数,若 为真命题,
为真命题,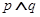 为假命题,则实数
为假命题,则实数 的取值范围为 .
的取值范围为 .
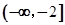
解析试题分析:本题先求出命题p,q为真命题时实数a的取值范围,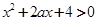 对一切
对一切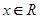 恒成立,则
恒成立,则 ,解得
,解得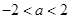 ,即命题
,即命题 ;函数
;函数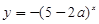 是减函数,则
是减函数,则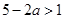 ,得
,得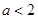 ,即命题
,即命题 .
. 为真命题,则
为真命题,则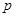 和
和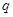 至少有一个为真,
至少有一个为真,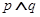 为假命题,则
为假命题,则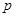 和
和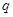 至少有一个为假,所以
至少有一个为假,所以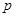 和
和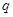 一真一假,但本题中
一真一假,但本题中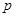 为真时,
为真时,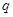 一定为真,故
一定为真,故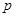 假且
假且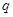 真,∴实数
真,∴实数 的取值范围是
的取值范围是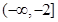 .
.
考点:逻辑连接词.

练习册系列答案
相关题目
 “若
“若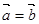 ,则
,则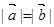 ”,则命题
”,则命题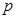 及其逆命题、否命题、逆否命题中,正确命题的个数是 .
及其逆命题、否命题、逆否命题中,正确命题的个数是 .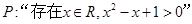 的否定
的否定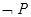 为__________
为__________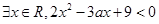 ”为假命题,则实数
”为假命题,则实数 的取值范围为 .
的取值范围为 .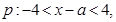
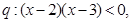 且
且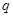 是
是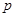 的充分而不必要条件,则
的充分而不必要条件,则 的取值范围为 .
的取值范围为 .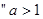 或
或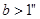 是
是 的 条件.
的 条件.  ,则
,则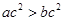 (
(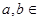 R)”否命题的真假性为 (从“真”、“假”中选填一个).
R)”否命题的真假性为 (从“真”、“假”中选填一个).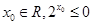 ”的否定是 。
”的否定是 。