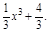题目内容
已知曲线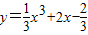 .
.(1)求曲线在点P(2,6)处的切线方程;
(2)求曲线过点P(2,6)的切线方程.
【答案】分析:(1)根据求导公式和法则求出函数的导数,再把x=2代入导函数求出切线的斜率,再代入点斜式化为一般式;
(2)由曲线方程设出切点的坐标,再求出切线的斜率,再把斜率和切点的坐标代入点斜式化简,由切线过点P再把P的坐标代入切线方程,求出切点的横坐标代入切线方程,最后化为一般式.
解答:解:(1)由题意得,y′=x2+2,
∴在点P(2,6)处的切线的斜率k=y′|x=2=6,
∴在点P(2,6)处的切线方程为:y-6=6(x-2)
即 6x-y-6=0,
(2)设曲线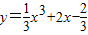 与过点P(2,6)的切线相切于点
与过点P(2,6)的切线相切于点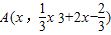 ,
,
则切线的斜率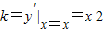 +2,
+2,
∴切线方程为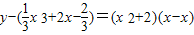 ,
,
即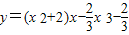 ①,
①,
∵点P(2,6)在切线上,∴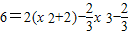 ,
,
即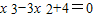 ,∴
,∴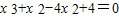 ,
,
∴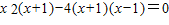 ,化简得
,化简得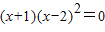
解得x=-1或x=2,代入①得,y=3x或y=6x-6,
故所求的切线方程为3x-y=0,6x-y-6=0.
点评:本题考查了导数的几何意义和“过”、“再”某点处的切线区别,关键是利用某点处的切线的斜率是该点出的导数值,以及切点在曲线上和切线上.
(2)由曲线方程设出切点的坐标,再求出切线的斜率,再把斜率和切点的坐标代入点斜式化简,由切线过点P再把P的坐标代入切线方程,求出切点的横坐标代入切线方程,最后化为一般式.
解答:解:(1)由题意得,y′=x2+2,
∴在点P(2,6)处的切线的斜率k=y′|x=2=6,
∴在点P(2,6)处的切线方程为:y-6=6(x-2)
即 6x-y-6=0,
(2)设曲线
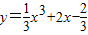 与过点P(2,6)的切线相切于点
与过点P(2,6)的切线相切于点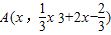 ,
,则切线的斜率
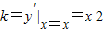 +2,
+2,∴切线方程为
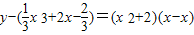 ,
,即
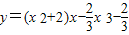 ①,
①,∵点P(2,6)在切线上,∴
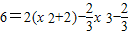 ,
,即
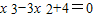 ,∴
,∴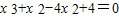 ,
,∴
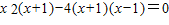 ,化简得
,化简得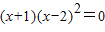
解得x=-1或x=2,代入①得,y=3x或y=6x-6,
故所求的切线方程为3x-y=0,6x-y-6=0.
点评:本题考查了导数的几何意义和“过”、“再”某点处的切线区别,关键是利用某点处的切线的斜率是该点出的导数值,以及切点在曲线上和切线上.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
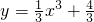 ,
,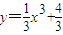 ,
,