题目内容
已知对任意平面向量 =(x,y),我们把
=(x,y),我们把 绕其起点A沿逆时针方向旋转θ角得到向量
绕其起点A沿逆时针方向旋转θ角得到向量 =(xcosθ-ysinθ,xsinθ+ycosθ),称为
=(xcosθ-ysinθ,xsinθ+ycosθ),称为 逆旋θ角到
逆旋θ角到 .
.
(1)把向量 =(2,-1)逆旋
=(2,-1)逆旋 角到
角到 ,试求向量
,试求向量 .
.
(2)设平面内函数y=f (x)图象上的每一点M,把 逆旋
逆旋 角到
角到 后(O为坐标原点),得到的N点的轨迹是曲线x2-y2=3,当函数F (x)=λ f (x)-|x-1|+2有三个不同的零点时,求实数λ的取值范围.
后(O为坐标原点),得到的N点的轨迹是曲线x2-y2=3,当函数F (x)=λ f (x)-|x-1|+2有三个不同的零点时,求实数λ的取值范围.
解:(1)由题意, =(2cos
=(2cos +sin
+sin ,2sin
,2sin -cos
-cos )=(
)=( );
);
(2)设M(x,y),N(x0,y0),则x02-y02=3
∵ 逆旋
逆旋 角到
角到 ,∴(xcos
,∴(xcos -ysin
-ysin ,xsin
,xsin +ycos
+ycos )=(x0,y0),
)=(x0,y0),
∴x0= ,y0=
,y0=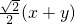 ,
,
∵x02-y02=3,∴可得y=- ,即f(x)=-
,即f(x)=-
函数F (x)=λ f (x)-|x-1|+2有三个不同的零点,等价于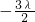 =x|x-1|-2x(x≠0)有三个不同实数解.
=x|x-1|-2x(x≠0)有三个不同实数解.
设g(x)=x|x-1|-2x= ,图象如图
,图象如图
∵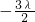 =x|x-1|-2x(x≠0)有三个不同实数解
=x|x-1|-2x(x≠0)有三个不同实数解
∴ ,且
,且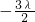 ≠0
≠0
∴ ,且λ≠0.
,且λ≠0.
分析:(1)利用新定义,结合向量 =(2,-1)逆旋
=(2,-1)逆旋 角到
角到 ,可求向量
,可求向量 ;
;
(2)由题意函数F (x)=λ f (x)-|x-1|+2有三个不同的零点,等价于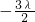 =x|x-1|-2x(x≠0)有三个不同实数解,结合函数的图象可得结论.
=x|x-1|-2x(x≠0)有三个不同实数解,结合函数的图象可得结论.
点评:本题考查新定义,考查数形结合的数学思想,考查学生的计算能力,属于基础题.
 =(2cos
=(2cos +sin
+sin ,2sin
,2sin -cos
-cos )=(
)=( );
);
(2)设M(x,y),N(x0,y0),则x02-y02=3
∵
 逆旋
逆旋 角到
角到 ,∴(xcos
,∴(xcos -ysin
-ysin ,xsin
,xsin +ycos
+ycos )=(x0,y0),
)=(x0,y0),∴x0=
 ,y0=
,y0=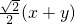 ,
,∵x02-y02=3,∴可得y=-
 ,即f(x)=-
,即f(x)=-
函数F (x)=λ f (x)-|x-1|+2有三个不同的零点,等价于
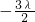 =x|x-1|-2x(x≠0)有三个不同实数解.
=x|x-1|-2x(x≠0)有三个不同实数解.设g(x)=x|x-1|-2x=
 ,图象如图
,图象如图∵
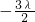 =x|x-1|-2x(x≠0)有三个不同实数解
=x|x-1|-2x(x≠0)有三个不同实数解∴
 ,且
,且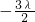 ≠0
≠0∴
 ,且λ≠0.
,且λ≠0.分析:(1)利用新定义,结合向量
 =(2,-1)逆旋
=(2,-1)逆旋 角到
角到 ,可求向量
,可求向量 ;
;(2)由题意函数F (x)=λ f (x)-|x-1|+2有三个不同的零点,等价于
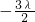 =x|x-1|-2x(x≠0)有三个不同实数解,结合函数的图象可得结论.
=x|x-1|-2x(x≠0)有三个不同实数解,结合函数的图象可得结论.点评:本题考查新定义,考查数形结合的数学思想,考查学生的计算能力,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 =(x,y),把
=(x,y),把 角得到向量
角得到向量 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 后得到点的轨迹是曲线
后得到点的轨迹是曲线 ,则原来曲线C的方程是____
,则原来曲线C的方程是____