题目内容
已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, .
.
(1)求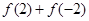 的值;
的值;
(2)求 的解析式;
的解析式;
(3)解关于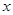 的不等式
的不等式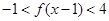 ,结果用集合或区间表示.
,结果用集合或区间表示.
(1)0
(2)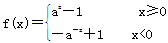
(3)当a>1时,不等式的解集为(1-loga2,1+loga5);当0<a<1时,不等式的解集为R.
解析试题分析:解 (1)∵f(x)是奇函数,∴f(-2)=-f(2),即f(2)+f(-2)=0.
(2)当x<0时,-x>0,∴f(-x)=a-x-1.
∵f(x)是奇函数,有f(-x)=-f(x),∴f(x)=-a-x+1(x<0).
∴所求的解析式为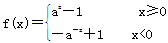 .
.
(3)不等式等价于 或
或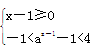 ,
,
即 或
或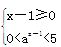 .
.
当a>1时,有 或
或 ,注意此时loga2>0,loga5>0,
,注意此时loga2>0,loga5>0,
可得此时不等式的解集为(1-loga2,1+loga5).
同理可得,当0<a<1时,不等式的解集为R.
综上所述,当a>1时,不等式的解集为(1-loga2,1+loga5);当0<a<1时,不等式的解集为R.
考点:不等式的应用
点评:解决的关键是对于奇偶性和单调性的应用,属于基础题。

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ;
; -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围; 是定义在R上的奇函数,又是周期为2的周期函数,当
是定义在R上的奇函数,又是周期为2的周期函数,当 时,
时, ,则
,则 的值为_____.
的值为_____.  是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则不等式
,则不等式 的解集是
.
的解集是
.