题目内容
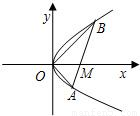
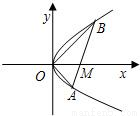
如图,直线l与抛物线y2=x交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,且y1y2=-1,
(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值。
(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值。
解:(1)设M点的坐标为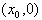 ,
,
直线l方程为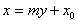 ,
,
代入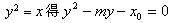 ,①
,①
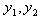 是此方程的两根,
是此方程的两根,
∴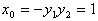 ,即M点的坐标为(1, 0)。
,即M点的坐标为(1, 0)。
(2)∵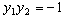 ,
,
∴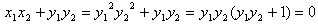 ,
,
∴OA⊥OB。
(3)由方程①,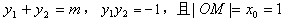 ,
,
于是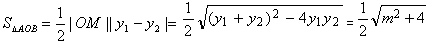 ≥1,
≥1,
∴当m=0时,△AOB的面积取最小值1。
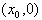 ,
,直线l方程为
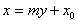 ,
,代入
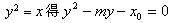 ,①
,①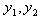 是此方程的两根,
是此方程的两根, ∴
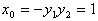 ,即M点的坐标为(1, 0)。
,即M点的坐标为(1, 0)。 (2)∵
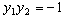 ,
, ∴
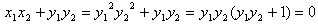 ,
,∴OA⊥OB。
(3)由方程①,
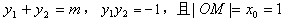 ,
,于是
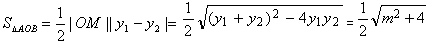 ≥1,
≥1,∴当m=0时,△AOB的面积取最小值1。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
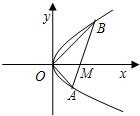 如图,直线l与抛物线y2=x交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,且y1y2=-1.
如图,直线l与抛物线y2=x交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,且y1y2=-1.(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值.
如图,直线l与抛物线y2=x交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,且y1y2=-1.
(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值.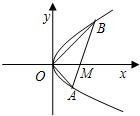
(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值.