题目内容
13．
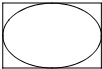如图所示，矩形长为3，宽为2，在矩形内随机撒200颗黄豆，数得落在椭圆内的黄豆数为160颗，依据此实验数据可以估计出椭圆的面积约为4.8．
分析 欲估计出椭圆的面积，可利用几何概型的概率模拟，只要利用椭圆的面积与矩形面积的比与落在椭圆内的黄豆数与所有黄豆数的比．
解答 解：黄豆落在椭圆内的概率为：$\frac{{S}_{椭圆}}{3×2}=\frac{160}{200}$
解得：S椭圆=4.8．
故答案为：4.8
点评 本题考查几何概型的应用（用来估计不规则图象的面积等）．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，称为几何概型．
练习册系列答案
相关题目
4．
随着经济发展带来的环境问题，我国很多城市提出了大力发展城市公共交通的理念，同时为了保证不影响市民的正常出行，就要求对公交车的数量必须进行合理配置．为此，某市公交公司在某站台随机对20名乘客进行了调查，其已候车时间情况如表（单位：分钟）
（1）画出已候车时间的频率分布直方图
（2）求这20名乘客的平均候车时间
（3）在这20名乘客中随机抽查一人，求其已候车时间不少于15分钟的概率．
随着经济发展带来的环境问题，我国很多城市提出了大力发展城市公共交通的理念，同时为了保证不影响市民的正常出行，就要求对公交车的数量必须进行合理配置．为此，某市公交公司在某站台随机对20名乘客进行了调查，其已候车时间情况如表（单位：分钟）| 组别 | 已候车时间 | 人数 |
| Ⅰ | [0，5） | 4 |
| Ⅱ | [5，10） | 6 |
| Ⅲ | [10，15） | 6 |
| Ⅳ | [15，20） | 3 |
| Ⅴ | [20，25] | 1 |
（2）求这20名乘客的平均候车时间
（3）在这20名乘客中随机抽查一人，求其已候车时间不少于15分钟的概率．
1．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（x，-2），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$+$\overrightarrow{b}$等于（ ）
| A． | （-3，1） | B． | （3，1） | C． | （2，1） | D． | （-2，-1） |
5．执行如图所示的程序框图，要使输出的S的值小于1，则输入的t值不能是下面的（ ）
| A． | 8 | B． | 9 | C． | 10 | D． | 11 |