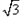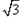题目内容
三角形的内角平分线定理是这样叙述的:三角形一个内角的平分线分对边所成的两条线段与这个角的两边对应成比例.已知在△ABC中,∠A=60°,∠A的平分线AD交边BC于点D,设AB=3,且 =
=
 +λ
+λ (λ∈R),则AD的长为( )
(λ∈R),则AD的长为( )A.2

B.

C.1
D.3
【答案】分析:作DG∥AB,DH∥AC,证明△ADH≌△ADG,可得AG=DH= AC,根据△BDH∽△BCA,可得BH=
AC,根据△BDH∽△BCA,可得BH= BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
解答: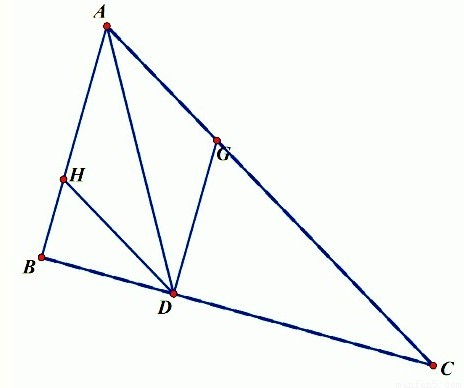 解:如图,作DG∥AB,DH∥AC,则向量
解:如图,作DG∥AB,DH∥AC,则向量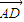 =
=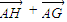 ,
,
∴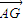 =
=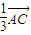 .
.
因为AD平分∠BAC,所以∠BAD=∠DAC=30°.
因为DG∥AB,所以∠ADH=30°=∠DAH,所以AH=DH,同理,AG=DG.
∴△ADH≌△ADG,∴AG=DH=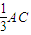 .
.
又因为△BDH∽△BCA,所以BH= BA=1,所以HA=HD=2,
BA=1,所以HA=HD=2,
根据等腰三角形知识可知AD=2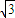 ,
,
故选A.
点评:本题考查向量知识的运用,考查三角形的全等与相似,属于中档题.
 AC,根据△BDH∽△BCA,可得BH=
AC,根据△BDH∽△BCA,可得BH= BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.
BA=1,从而HA=HD=2,根据等腰三角形知识可求AD的长.解答:
 解:如图,作DG∥AB,DH∥AC,则向量
解:如图,作DG∥AB,DH∥AC,则向量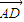 =
=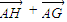 ,
,∴
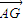 =
=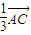 .
.因为AD平分∠BAC,所以∠BAD=∠DAC=30°.
因为DG∥AB,所以∠ADH=30°=∠DAH,所以AH=DH,同理,AG=DG.
∴△ADH≌△ADG,∴AG=DH=
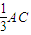 .
.又因为△BDH∽△BCA,所以BH=
 BA=1,所以HA=HD=2,
BA=1,所以HA=HD=2,根据等腰三角形知识可知AD=2
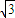 ,
,故选A.
点评:本题考查向量知识的运用,考查三角形的全等与相似,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,则AD的长为( )
,则AD的长为( ) B.
B. =
=
 +λ
+λ (λ∈R),则AD的长为
(λ∈R),则AD的长为
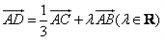 ,则AD的长为
,则AD的长为