题目内容
已知抛物线 :
: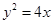 的焦点为
的焦点为 ,直线
,直线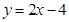 与
与 交于
交于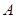 、
、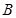 两点.则
两点.则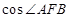 ="________."
="________."
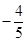
解析试题分析:由题意可知,y²=4x=(2x-4)²,联立方程组消元法得到,x²-5x+4=0,所以x=1,x=4,A(1,-2),B(4,4),2p=4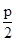 =1,F(1,0),所以AB=3
=1,F(1,0),所以AB=3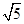 ,AF=2,BF=5,则利用三角形中的余弦定理
,AF=2,BF=5,则利用三角形中的余弦定理
cosAFB=-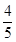 ,故答案为-
,故答案为-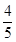 。
。
考点:本题主要考查了抛物线的定义的运用。直线与抛物线的位置关系的运用。
点评:解决该试题的关键是设出点,联立方程组,运用韦达定理得到根与系数的关系,结合坐标得到角AFB的余弦值的求解。

练习册系列答案
相关题目
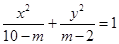 ,若其长轴在
,若其长轴在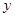 轴上.焦距为
轴上.焦距为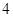 ,则
,则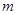 等于___________。
等于___________。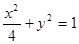 的两个焦点分别为
的两个焦点分别为 ,过
,过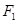 作垂直于
作垂直于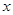 轴的直线与椭圆相交,其中一个交点为
轴的直线与椭圆相交,其中一个交点为 ,则
,则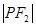 = .
= . 是双曲线C:
是双曲线C: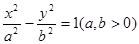 的左焦点,
的左焦点,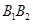 是双曲线的虚轴,
是双曲线的虚轴,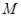 是
是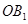 的中点,过
的中点,过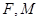 的直线交双曲线C于
的直线交双曲线C于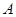 ,且
,且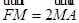 ,则双曲线C离心率是____
,则双曲线C离心率是____ 焦点的直线与抛物线交于
焦点的直线与抛物线交于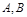 两点,
两点,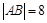 ,则线段
,则线段 的中点横坐标为 。
的中点横坐标为 。 为过抛物线
为过抛物线 焦点
焦点 的一条弦,设
的一条弦,设 ,以下结论正确的是_______
,以下结论正确的是_______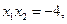 且
且 ;
;  的最小值为
的最小值为 ;
;  为直径的圆与
为直径的圆与 轴相切;
轴相切;  与双曲线
与双曲线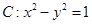 有且只有一个公共点,则
有且只有一个公共点,则 =
= 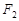 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,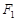 的直线MF1是圆
的直线MF1是圆