Question

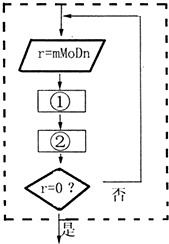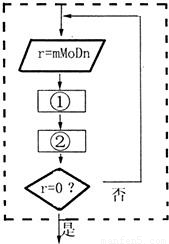
辗转相除法的基本步骤是用较大的数（用变量m表示）除以较小的数（用变量n表示）
除式为m=n•q+r（0≤r＜n），这是一个反复执行的循环过程，如图个循环结构的程序框图，则①、②两处应依次填写

m=n

、

n=r

．

Answer 1

分析：辗转相除法可以用来求两个数的最大公因数原理是先用较大的数（用变量m表示）除以较小的数（用变量n表示）商为q余数为r若r=0则最大公因数为q否则再用n除以r商为q′余数r′若r′=0则最大公因数q′一直这样做下去直至r′=0则此时的商即为最大公因数．

解答：解：由分析中可知辗转相除法实际上就是用较大数除以较小数如果能除尽则商就是两数的最大公因数否则再用较小的数除以前一次的余数如果能除尽则商就是两数的最大公因数否则继续前一次的过程．因此设计成循环结构的程序框图只需将除数赋予被除数余数赋予除数即可．
故答案为：m=n，n=r

点评：此题主要考查了有关辗转相除法的理论知识，关键是要理解辗转相除法的理论依据和求解要点！