题目内容
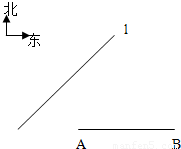
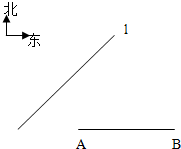 如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(
如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(| 6 |
| 2 |
(Ⅰ)求公路l所在直线的方程;
(Ⅱ)在公路l上有一站点M到A,B两工厂路程之和最小,现要建一条经过M的环行公路,使公路上每一点到A,B两工厂路程之和相等,求环行公路所在曲线的方程;
(Ⅲ)开发区内有一物资储藏库C位于B工厂西北距B工厂
| 2 |
分析:(Ⅰ)以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),设直线l的方程:y=x+m,由点A到l的距离为(
-
)km可得关于m的方程.解出m后即得l的方程;
(Ⅱ)设P(x,y)设所求曲线上任意一点,则由题意知点P(x,y)的轨迹是以A,B为焦点,且长轴最短的椭圆.设此椭圆的方程为
+
=1,则方程组
有唯一解,消元后
令△=0可得b2=4,进而得a2=8;
(Ⅲ)由题意知C(1,1),在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小,即在
+
=1上求一点N,使|NC|+|NB|最小.当N为直线lAC:x-3y+2=0与椭圆
+
=1交点之一时,|NC|+|NB|最小,通过解方程组可得求;
| 6 |
| 2 |
(Ⅱ)设P(x,y)设所求曲线上任意一点,则由题意知点P(x,y)的轨迹是以A,B为焦点,且长轴最短的椭圆.设此椭圆的方程为
| x2 |
| b2+4 |
| y2 |
| b2 |
|
令△=0可得b2=4,进而得a2=8;
(Ⅲ)由题意知C(1,1),在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小,即在
| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 8 |
| y2 |
| 4 |
解答: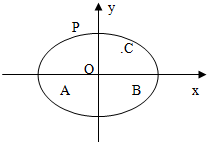 解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),
解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),
(Ⅰ) 设直线l的方程:y=x+m,则由题意知m>2,直线l在点A的右上方,
=
-
,|-2+m|=2
-2,
由m>2得m=2
,∴直线l的方程:y=x+2
;
(Ⅱ)设P(x,y)设所求曲线上任意一点,则由题意知点P(x,y)的轨迹是以A,B为焦点,且长轴最短的椭圆.
设此椭圆的方程为
+
=1,则方程组
有唯一解,
b2(y-2
)2+(b2+4)y2=b2(b2+4),(2b2+4)y2-4
b2y-b2(b2-8)=0,
△=48b4+8b2(b2-8)(b2+2)=4b2(b4-16)=0,b2=4,a2=8,
所求椭圆的方程为
+
=1;
(Ⅲ)由题意知C(1,1),
在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小,
即在
+
=1上求一点N,使|NC|+|NB|最小.
显然,当N为直线lAC:x-3y+2=0与椭圆
+
=1交点之一时,|NC|+|NB|最小,
由方程组
,得(3y-2)2+2y2-8=11y2-12y-4=0,
解得
或
,
当N(
,
)时,(|NC|+|NB|)min=2a-|AC|=16-
,
 解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),
解:以A,B所在直线为x轴,中点为原点,建立直角坐标系,则A(-2,0),B(2,0),(Ⅰ) 设直线l的方程:y=x+m,则由题意知m>2,直线l在点A的右上方,
| |-2+m| | ||
|
| 6 |
| 2 |
| 3 |
由m>2得m=2
| 3 |
| 3 |
(Ⅱ)设P(x,y)设所求曲线上任意一点,则由题意知点P(x,y)的轨迹是以A,B为焦点,且长轴最短的椭圆.
设此椭圆的方程为
| x2 |
| b2+4 |
| y2 |
| b2 |
|
b2(y-2
| 3 |
| 3 |
△=48b4+8b2(b2-8)(b2+2)=4b2(b4-16)=0,b2=4,a2=8,
所求椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅲ)由题意知C(1,1),
在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小,
即在
| x2 |
| 8 |
| y2 |
| 4 |
显然,当N为直线lAC:x-3y+2=0与椭圆
| x2 |
| 8 |
| y2 |
| 4 |
由方程组
|
解得
|
|
当N(
-4+12
| ||
| 11 |
6+4
| ||
| 11 |
| 10 |
点评:本题考查直线与椭圆的位置关系、圆锥曲线中的最值问题、椭圆在实际中的应用,考查学生分析解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
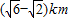 .建立适当的坐标系,解决下列问题:
.建立适当的坐标系,解决下列问题: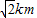 ,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.
,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.