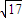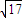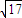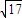题目内容
设α∈{1,2,3,
,-1},则使y=xα为奇函数且在(0,1)上图象在直线y=x上方的α值为
| 1 | 2 |
-1
-1
.分析:按照幂函数的性质,当指数大于零时,在第一象限为增函数;当指数小于零时,在第一象限为减函数,其它象限结合奇偶性解决,可得到答案.
解答:解:∵y=xα为奇函数且在(0,1)上图象在直线y=x上方
∴y=xα为奇函数且在(0,+∞)上单调递减
根据幂函数的性质,
当α=-1时,y=xα为奇函数且在(0,+∞)上单调递减
故答案为:-1
∴y=xα为奇函数且在(0,+∞)上单调递减
根据幂函数的性质,
当α=-1时,y=xα为奇函数且在(0,+∞)上单调递减
故答案为:-1
点评:本题主要考查幂函数的图象和性质,涉及到函数的奇偶性和单调性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 |=1,|
|=1,| |=2,|
|=2,| |=3,且
|=3,且
 ,-1},则使y=xα为奇函数且在(0,1)上图象在直线y=x上方的α值为 .
,-1},则使y=xα为奇函数且在(0,1)上图象在直线y=x上方的α值为 .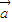 |=1,|
|=1,| |=2,|
|=2,|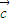 |=3,且
|=3,且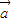 •
•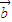 =0,则(
=0,则(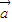 +2
+2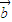 )
)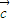 的最小值为( )
的最小值为( )