Question

已知甲、乙两个工厂在今年的1月份的利润都是6万元，且甲厂在2月份的利润是14万元，乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润（万元）与月份x之间的函数关系式分别符合下列函数模型：f（x）=a₁x²+b₁x+6，g（x）=a₂•3^x+b₂，（a₁，a₂，b₁，b₂∈R）．
（1）求甲、乙两个工厂今年5月份的利润；
（2）在同一直角坐标系下画出函数f（x）与g（x）的草图，并根据草图比较今年甲、乙两个工厂的利润的大小情况．

Answer 1

分析：（1）先根据条件结合函数模型，求得函数，进而再求相应的函数值．
（2）一个二次函数型，一个是指数函数型，可按照提供的几个已知点，结合模型特点作出图象，根据图象找出相等点来，图象在上方的为利润大，在下方的为利润小．

解答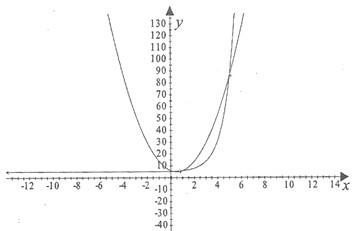：解：（1）依题意：由

f(1)=6 f(2)=14

，有

a1+b1=0 4a1+2b1=8

，解得：a₁=4，b₁=-4
∴f（x）=4x²-4x+6；（2分）
由

g(1)=6 g(2)=8

，有

3a2+b2=6 9a2+b2=8

，
解得：a2=

1

3

，b2=5
∴g(x)=

1

3

•3x+5=3x-1+5．（4分）
所以甲在今年5月份的利润为f（5）=86万元，
乙在今年5月份的利润为g（5）=86万元，
故有f（5）=g（5），即甲、乙两个工厂今年5月份的利润相等．（6分）
（2）作函数图象如图所示：
从图中，可以看出今年甲、乙两个工厂的利润：
当x=1或x=5时，有f（x）=g（x）；
当1＜x＜5时，有f（x）＞g（x）；
当5＜x≤12时，有f（x）＜g（x）；（12分）

点评：本题是一道应用题，是一道很常规的题，考查了解应用题的基本思路：先根据相关条件建立模型，再应用模型，特别在第二问，又将图象引入，两个模型的优劣一看就知．