题目内容
函数 ,过曲线
,过曲线 上的点
上的点 的切线方程为
的切线方程为 .
.
(1)若 在
在 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)的条件下,求 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函数 在区间[-2,1]上单调递增,求实数b的取值范围.
在区间[-2,1]上单调递增,求实数b的取值范围.
解 (1)由f(x)=x3+ax2+bx+c求导数得f′(x)=3x2+2ax+b.过y=f(x)上点P(1,f(1))的切线方程为y-f(1)=f′(1)(x-1),
即y-(a+b+c+1)=(3+2a+b)(x-1).而过y=f(x)上点P(1,f(1))的切线方程为y=3x+1.故即
∵y=f(x)在x=-2时有极值,故f′(-2)=0.∴-4a+b=-12. ③
由①②③联立解得a=2,b=-4,c=5,∴f(x)=x3+2x2-4x+5.
(2)f′(x)=3x2+4x-4=(3x-2)(x+2),令f′(x)=0,解得x=或x=-2.
列下表:
|
x |
-3 |
(-3,-2) |
-2 |
(-2,) |
(,1) |
1 |
|
|
f′(x) |
|
+, |
0 |
- |
0 |
+ |
|
|
f(x) |
8 |
|
极大值 |
|
极小值 |
|
4 |
∴f(x)的极大值为f(-2)=13,极小值为f()=.又∵f(-3)=8,f(1)=4,
∴f(x)在[-3,1]上的最大值为13.
(3)y=f(x)在[-2,1]上单调递增.又f′(x)=3x2+2ax+b.由(1)知2a+b=0.
∴f′(x)=3x2-bx+b.依题意在[-2,1]上恒有f′(x)≥0,即3x2-bx+b≥0在[-2,1]上恒成立,
当x=≥1时,即b≥6时,[f′(x)]min=f′(1)=3-b+b>0,∴b≥6时符合要求.
当x=≤-2时,即b≤-12时,[f′(x)]min=f′(-2)=12+2b+b≥0,∴b不存在.
当-2<<1即-12<b<6时,[f′(x)]min=≥0,∴0≤b<6,
综上所述b≥0.
【解析】略


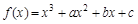 ,过曲线
,过曲线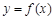 上的点
上的点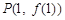 的切线方程为
的切线方程为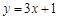
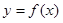 在
在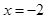 时有极值,求
时有极值,求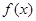 的表达式;
的表达式;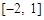 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.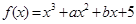 ,过曲线
,过曲线 上的点
上的点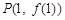 的切线斜率为3.
的切线斜率为3.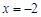 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;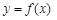 在
在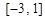 上最大值;
上最大值; ,过曲线
,过曲线 上的点
上的点 的切线方程为
的切线方程为 .
. 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式; 在
在 上最大值;
上最大值; 上单调递增,求b的取值范
上单调递增,求b的取值范