题目内容
设｛an｝为递增等差数列，前三项的和为12，前三项的积为48，则它的首项为
| A．1 | B．2 | C．4 | D．6 |
B
解析试题分析：设等差数列｛an｝的公差为d（d>0）,∵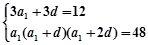
，∴
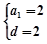或
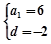（舍去），故选B
考点：本题考查了等差数列的通项公式
点评：熟练运用等差数列的通项公式是解决此类问题的关键，解题时注意审题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知数列
是等差数列，若
，则数列的公差等于
| A．1 | B．3 | C．5 | D．6 |
已知数列
为等差数列且
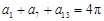，则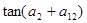
的值为（ ）
A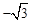． | B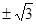． | C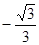． | D． |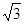
数列
中，a1=－6，且a n+1 =an+ 3，则这个数列的第30项为（ ）
| A．81 | B．1125 | C．87 | D．99 |
已知等差数列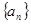
的公差为2,若
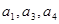成等比数列, 则
=（ ）
A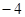． | B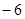． | C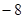． | D． |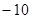
已知数列{an}满足a1＝0，an＋1＝
(n∈N*)，则a20等于( )
| A．0 | B．－ |
| C． | D． |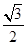
等差数列{an}和{bn}的前n项和分别为Sn和Tn，且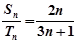
，则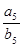
（ ）
A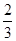． | B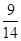． | C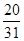． | D． |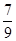
已知等差数列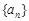
公差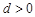
，前n项和为
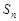．则“
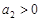”是“数列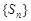
为递增数列”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充也不必要条件 |
数列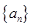
的首项为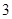
，
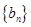为等差数列且
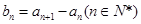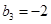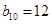.若则
，
，则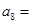
（ ）
| A．0 | B．3 | C．8 | D．11 |