题目内容
若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60°的菱形,则该棱柱的体积等于( )
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
分析:先求侧棱与底面所成角的余弦,然后求出棱柱的高,再求棱柱的体积.
解答: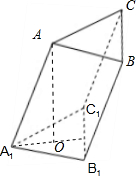 解:如图在三棱柱ABC-A1B1C1中,设∠AA1B1=∠AA1C1=60°,
解:如图在三棱柱ABC-A1B1C1中,设∠AA1B1=∠AA1C1=60°,
由条件有∠C1A1B1=60°,作AO⊥面A1B1C1于点O,
则cos∠AA1O=
=
=
=
∴sin∠AA1O=
∴AO=AA1•sin∠AA1O=
∴VABC-A1B1AOC1=S△A1B1C1•AO=
×2×2×sin600×
=2
故选B.
 解:如图在三棱柱ABC-A1B1C1中,设∠AA1B1=∠AA1C1=60°,
解:如图在三棱柱ABC-A1B1C1中,设∠AA1B1=∠AA1C1=60°,由条件有∠C1A1B1=60°,作AO⊥面A1B1C1于点O,
则cos∠AA1O=
| cos∠AA1B1 |
| cos∠B1A1O |
| cos600 |
| cos300 |
| 1 | ||
|
| ||
| 3 |
∴sin∠AA1O=
| ||
| 3 |
2
| ||
| 3 |
∴VABC-A1B1AOC1=S△A1B1C1•AO=
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
故选B.
点评:此题重点考查立体几何中的最小角定理和柱体体积公式,同时考查空间想象能力;具有较强的空间想象能力,准确地画出图形是解决此题的前提,熟悉最小角定理并能准确应用是解决此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
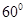 的菱形,则该棱柱的体积等于
( )
的菱形,则该棱柱的体积等于
( )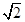 B.
B. 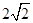 C.
C. 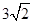 D.
D. 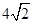
 的菱形,则该棱柱的体积等于
( )
的菱形,则该棱柱的体积等于
( )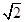 B.
B. 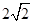 C.
C. 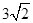 D.
D. 