题目内容
对于正实数α,Mα为满足下述条件的函数f(x)构成的集合:?x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)-f(x1)<α(x2-x1).下列结论中正确的是( )
分析:对于-α(x2-x1)<f(x2)-f(x1)<α(x2-x1).变形有-α<
<α,令k=
,不妨设f(x)∈Mα1,g(x))∈Mα2,利用不等式的性质可得f(x)+g(x)∈Mα1+α2.从而得出正确答案.
| f(x 2)-f(x 1) |
| x 2-x 1 |
| f(x 2)-f(x 1) |
| x 2-x 1 |
解答:解:对于-α(x2-x1)<f(x2)-f(x1)<α(x2-x1),
即有-α<
<α,令k=
,
有-α<k<α,不妨设f(x)∈Mα1,g(x))∈Mα2,
即有-α1<kf<α1,-α2<kg<α2,因此有-α1-α2<kf+kg<α1+α2,
因此有f(x)+g(x)∈Mα1+α2.
故选C.
即有-α<
| f(x 2)-f(x 1) |
| x 2-x 1 |
| f(x 2)-f(x 1) |
| x 2-x 1 |
有-α<k<α,不妨设f(x)∈Mα1,g(x))∈Mα2,
即有-α1<kf<α1,-α2<kg<α2,因此有-α1-α2<kf+kg<α1+α2,
因此有f(x)+g(x)∈Mα1+α2.
故选C.
点评:本题考查的是元素与集合关系的判断、进行简单的合情推理、函数恒成立问题,在能力上主要考查对新信息的理解力及解决问题的能力.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
[ ]
A.若f(x)∈ ,g(x)∈
,g(x)∈ ,则f(x)·g(x)∈
,则f(x)·g(x)∈
B.若f(x)∈ ,g(x)∈
,g(x)∈ ,且g(x)≠0 则
,且g(x)≠0 则
C.若f(x)∈ ,g(x)∈
,g(x)∈ ,则f(x)+g(x)∈
,则f(x)+g(x)∈
D.若f(x)∈ ,g(x)∈
,g(x)∈ ,且α1>α2,则f(x)-g(x)∈
,且α1>α2,则f(x)-g(x)∈
 ,g(x)∈
,g(x)∈ ,则f(x)·g(x)∈
,则f(x)·g(x)∈
B.若f(x)∈
 ,g(x)∈
,g(x)∈ ,且g(x)≠0 则
,且g(x)≠0 则
C.若f(x)∈
 ,g(x)∈
,g(x)∈ ,则f(x)+g(x)∈
,则f(x)+g(x)∈
D.若f(x)∈
 ,g(x)∈
,g(x)∈ ,且α1>α2,则f(x)-g(x)∈
,且α1>α2,则f(x)-g(x)∈
对于正实数α,记Mα为满足下述条件的函数 构成的集合:存在
构成的集合:存在 ,且
,且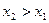 ,有
,有 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.若 ,则 ,则 |
B.若 ,且 ,且 ,则 ,则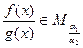 |
C.若 ,则 ,则 |
D.若 ,且 ,且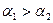 ,则 ,则 |
 构成的集合:存在
构成的集合:存在 ,且
,且 ,有
,有 ,下列结论中正确的是( )
,下列结论中正确的是( ) ,则
,则
 ,则
,则

 ,则
,则
 x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)- f(x1)<α(x2-x1)下列结论中正确的是
x1,x2∈R且x2>x1,有-α(x2-x1)<f(x2)- f(x1)<α(x2-x1)下列结论中正确的是