题目内容
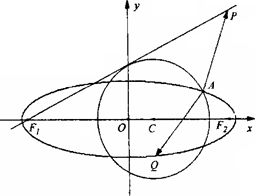
已知点P(4，4)，圆C：(x－m)2＋y2＝5(m＜3)与椭圆E：
有一个公共点A(3，1)，F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．
(Ⅰ)求m的值与椭圆E的方程．
(Ⅱ)设Q为椭圆E上的一个动点，求
的取值范围．
答案：
解析：
解析：
|
解：(Ⅰ)点A代入圆C方程， 得 设直线PF1的斜率为k，则PF1： ∵直线PF1与圆C相切，∴ 解得 当k＝ 当k＝ ∴c＝4．F1(－4，0)，F2(4，0)． 4分 2a＝AF1＋AF2＝ 椭圆E的方程为： (Ⅱ) ∵ 而 则 ∴ |
．∵m＜3，∴m＝1．圆C：
． 1分
，即
．
．
． 2分
时，直线PF1与x轴的交点横坐标为
，不合题意，舍去．
时，直线PF1与x轴的交点横坐标为－4，
，
，a2＝18，b2＝2．
． 6分
，设Q(x，y)，
，
． 8分
，
，∴－18≤6xy≤18．
的取值范围是[0，36]． 10分
的取值范围是[－6，6]．
的取值范围是[－12，0]． 12分
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
＝1(a＞b＞0)有一个公共点A(3，1)，F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．
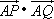的取值范围．
(a＞b＞0)有一个公共点A(3，1)．F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．
的取值范围．
(a＞b＞0)有一个公共点A(3，1)，F1、F2分别是椭圆的左、右焦点，直线PF1与圆C相切．
的取值范围．
与椭圆E：
有一个公共点A(3，1)，F1．F2分别是椭圆的左．右焦点，直线PF1与圆C相切．
的范围．