题目内容
某商人如果将进货单价为8元的商品按每件10元出售,每天可销售100件,现在他采用提高售价,减少进货量的办法增加利润.已知这种商品每件销售价提高1元,销售量就要减少10件,问他将销售价每件定为多少元时,才能使得每天所赚的利润最大.销售价定为多少元时,才能保证每天所赚的利润在300元以上?
答案:略
解析:
提示:
解析:
|
设每件提高 x元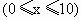 ,即每件获利润(2+x)元,则每天可销售 ,即每件获利润(2+x)元,则每天可销售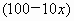 件,每天获总利润为y元,由题意有 件,每天获总利润为y元,由题意有
当 ∴当售价定为14元时,每天所赚利润最大为360元. 要使每天所赚的利润在300元以上,则有 即 故每件定价在 |
提示:
|
每天所获利润等于每件的利润与销售量之积,销售量随单价的提高而减少,可以根据题意把每天所获利润表示为每件提高售价的函数,转化为求函数的最值问题. |

练习册系列答案
相关题目
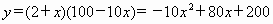 .
.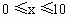 ,
,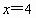 时,y取得最大值360.
时,y取得最大值360.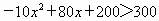 ,
,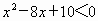 ,解得
,解得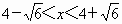 .
.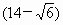 元到
元到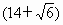 元之间时,能确保每天的利润在300元以上.
元之间时,能确保每天的利润在300元以上.