题目内容
由一个数列中部分项按原来次序排列的数列叫做这个数列的子数列,试在无穷等比数列 ,
, ,
, ,…中找出一个无穷等比的子数列,使它所有项的和为
,…中找出一个无穷等比的子数列,使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .
【答案】分析:设此子数列的首项为a1=( )m,公比为q=(
)m,公比为q=( )r,所有各项之和为
)r,所有各项之和为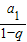 =
=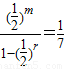 ,由此能求出此子数列通项公式.
,由此能求出此子数列通项公式.
解答:解:∵无穷等比数列 ,
, ,
, ,…中一个无穷等比的子数列所有项的和为
,…中一个无穷等比的子数列所有项的和为 ,
,
∴此子数列的首项为a1=( )m,公比为q=(
)m,公比为q=( )r,
)r,
所有各项之和为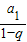 =
=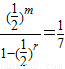 ,
,
整理,得2m-r(2r-1)=7,
解得m=r=3.
∴a1=q=( )3=
)3= ,
,
∴此子数列通项公式为an=a1qn-1=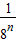 .
.
故答案为:an=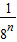 .
.
点评:本题考查数列通项公式的求法,解题的关键是正确理解子数列的含义,准确设出子数列的首项和公比,知道等比数列中所有各项之和为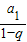 .
.
 )m,公比为q=(
)m,公比为q=( )r,所有各项之和为
)r,所有各项之和为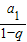 =
=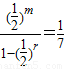 ,由此能求出此子数列通项公式.
,由此能求出此子数列通项公式.解答:解:∵无穷等比数列
 ,
, ,
, ,…中一个无穷等比的子数列所有项的和为
,…中一个无穷等比的子数列所有项的和为 ,
,∴此子数列的首项为a1=(
 )m,公比为q=(
)m,公比为q=( )r,
)r,所有各项之和为
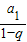 =
=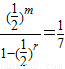 ,
,整理,得2m-r(2r-1)=7,
解得m=r=3.
∴a1=q=(
 )3=
)3= ,
,∴此子数列通项公式为an=a1qn-1=
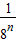 .
.故答案为:an=
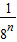 .
.点评:本题考查数列通项公式的求法,解题的关键是正确理解子数列的含义,准确设出子数列的首项和公比,知道等比数列中所有各项之和为
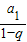 .
. 
练习册系列答案
相关题目
 ,
, ,
, ,…中找出一个无穷等比的子数列,使它所有项的和为
,…中找出一个无穷等比的子数列,使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .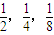 ,…中找出一个无穷等比的子数列(由原数列中部分项按原来次序排列的数列),使它所有项的和为
,…中找出一个无穷等比的子数列(由原数列中部分项按原来次序排列的数列),使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .