题目内容
若关于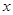 的不等式
的不等式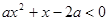 的解集中有且仅有4个整数解,则实数
的解集中有且仅有4个整数解,则实数 的取值范围是 .
的取值范围是 .
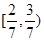
解析试题分析:当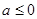 时,不等式
时,不等式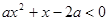 的解集中有无数个整数解,因此
的解集中有无数个整数解,因此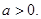 设
设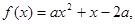 因为
因为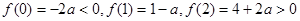 假若a>1,则f(1)=1-a<0,4个整数解应为1,0,-1,-2,而f(-2)=4a-2-2a=2a-2>0,矛盾,所以假设错误,故0<a≤1
假若a>1,则f(1)=1-a<0,4个整数解应为1,0,-1,-2,而f(-2)=4a-2-2a=2a-2>0,矛盾,所以假设错误,故0<a≤1
所以4个整数解应为0,-1,-2,-3.所以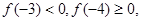 实数
实数 的取值范围是
的取值范围是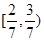 .
.
考点:一元二次不等式的整数解

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
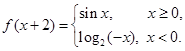 ,则
,则 = .
= .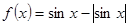 的性质,
的性质,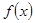 是以
是以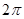 为周期的周期函数 ②
为周期的周期函数 ②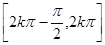 ,
,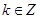
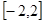 ④
④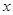 的取值集合为
的取值集合为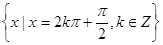
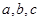 为正实数,
为正实数,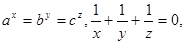 则
则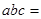 .
.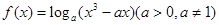 在区间(
在区间( )内单调递增,则a的取值范围是
)内单调递增,则a的取值范围是 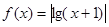 ,若
,若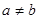 且
且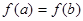 ,则
,则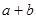 的取值范围是
的取值范围是 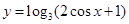 ,
,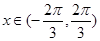 的值域是 .
的值域是 .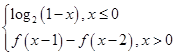 ,则f(2 013)=________.
,则f(2 013)=________.