题目内容
“x＞0”是“x-2＞0”的（ ）
分析：利用充分条件和必要条件的定义判断．
解答：解：由x-2＞0得x＞2．
当x=1时，满足x＞0，但x＞2不成立．
当x＞2时一定有x＞0成立．
所以“x＞0”是“x-2＞0”的必要不充分条件．
故选B．
当x=1时，满足x＞0，但x＞2不成立．
当x＞2时一定有x＞0成立．
所以“x＞0”是“x-2＞0”的必要不充分条件．
故选B．
点评：本题主要考查充分条件和必要条件的应用，比较基础．
练习册系列答案
相关题目
函数y=
+
的定义域是（ ）
| (x+1)0 | ||
|
| 1-6x2+x-2 |
| A、{x|-2≤x＜0} |
| B、{x|-2≤x＜0且x≠-1} |
| C、{x|x≤-2} |
| D、{x|x≥1} |
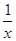≥2”的( )