题目内容
在 中,内角
中,内角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.
(Ⅰ)若 ,
, ,求
,求 的外接圆的面积;
的外接圆的面积;
(Ⅱ)若 ,
, ,求
,求 的面积.
的面积.
(Ⅰ)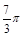 ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)先利用余弦定理求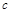 ,然后再利用正弦定理求得外接圆半径,最后求得外接圆面积.
,然后再利用正弦定理求得外接圆半径,最后求得外接圆面积.
(Ⅱ)由三角形内角和定理及已知条件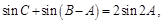 消去
消去 化简得
化简得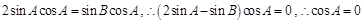 或
或 再分
再分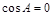 和
和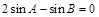 两种情况:当
两种情况:当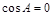 时,
时,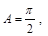 又
又 且
且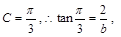 即
即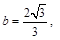 此时
此时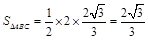 ;当
;当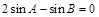 时,由正弦定理得
时,由正弦定理得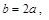 又
又 且
且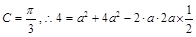 (或得到
(或得到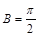 求解),解得
求解),解得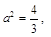 此时
此时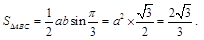
试题解析:(Ⅰ)由已知及余弦定理得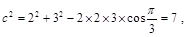 则
则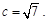 设外接圆半径为
设外接圆半径为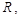 由正弦定理知
由正弦定理知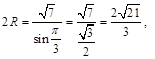 从而
从而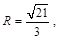 故外接圆的面积为
故外接圆的面积为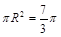 . 5分
. 5分
(Ⅱ)
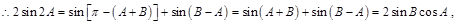
即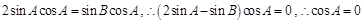 或
或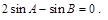
当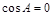 时,
时,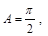 又
又 且
且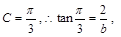 即
即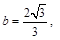 此时
此时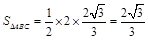 ;
;
当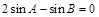 时,由正弦定理得
时,由正弦定理得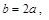 又
又 且
且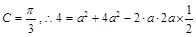 (或得到
(或得到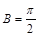 求解),解得
求解),解得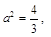 此时
此时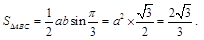
综上知 12分
12分
考点:应用正余弦定理解三角形、求三角形的面积.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 中,设内角
中,设内角 的对边分别为
的对边分别为 ,向量
,向量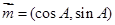 ,向量
,向量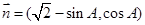 ,若
,若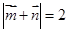
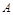 的大小;
的大小;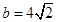 ,且
,且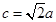 ,求
,求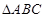 的角
的角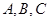 的对边分别为
的对边分别为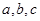 ,已知
,已知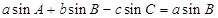 .
.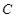 ;
; ,
,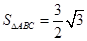 ,求
,求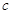 的值.
的值. 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
. ,
,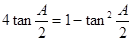 .
.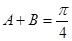 ;
;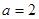 ,求c和ΔABC的面积.
,求c和ΔABC的面积. 是
是 的内角,
的内角, 分别是其对边长,且
分别是其对边长,且 .
. ,求
,求 的长;
的长; 的对边
的对边 ,求
,求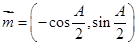 ,
,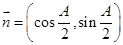 ,
,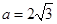 ,且
,且 .
.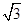 ,求b+c的值;
,求b+c的值; 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知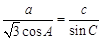 ,
, 的大小;
的大小; ,求
,求 的取值范围.
的取值范围. 海里的速度向正北方向航行,
海里的速度向正北方向航行,