题目内容
(07年浙江卷文)已知点O在二面角α-AB-β的棱上,点P在α内,且∠POB=45°.若对于β内异于O的任意一点Q,都有∠POQ≥45°,则二面角α-AB-β的取值范围是_________.
答案: ![]()
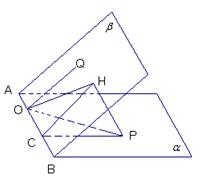
解析:若二面角α-AB-β的大小为锐角,则过点P向平面![]() 作垂线,设垂足为H.
作垂线,设垂足为H.
过H作AB的垂线交于C,连PC、CH、OH,则![]() 就是所求二面角的平面角.
就是所求二面角的平面角.
根据题意得![]() ,由于对于β内异于O的任意一点Q,都有
,由于对于β内异于O的任意一点Q,都有
∠POQ≥45°,∴![]() ,设PO=
,设PO=![]() ,则
,则![]()
又∵∠POB=45°,∴OC=PC=![]() ,而在
,而在![]() 中应有
中应有
PC>PH ,∴显然矛盾,故二面角α-AB-β的大小不可能为锐角。
即二面角![]() 的范围是
的范围是![]() 。
。
若二面角α-AB-β的大小为直角或钝角,则由于∠POB=45°,结合图形容易判断对于β内异于O的任意一点Q,都有∠POQ≥45°。
即二面角![]() 的范围是
的范围是![]() 。
。
【高考考点】二面角的求法及简单的推理判断能力
【易错点】:画不出相应的图形,从而乱判断。
【备考提示】:无论解析几何还是立体几何,借助于图形是我们解决问题的一个重要的方法,它可以将问题直观化,从而有助于问题的解决。

练习册系列答案
相关题目