题目内容
过椭圆
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点，若
，则椭圆的离心率e= ．
【答案】分析：设椭圆的左准线为l，设A、B两点在l上的射影分别为C、D，连接AC、BD，过点B作BG⊥AC利用圆锥曲线的统一定义，再结合直角△ABG中，∠BAG=60°，可求出边之间的长度之比，可得离心率的值．
解答：
解：如图，设设椭圆的左准线为l，过A点作AC⊥l于C，
过点B作BD⊥l于D，再过B点作BG⊥AC于G，
直角△ABG中，∠BAG=60°，所以AB=2AG，…①
由圆锥曲线统一定义得：
，
∵
∴AC=2BD
直角梯形ABDC中，AG=AC-BD=
…②
①、②比较，可得AB=AC，
又∵
∴
答：所求的离心率为
点评：运用圆锥曲线的统一定义，结合解含有60°的直角三角形，求椭圆的离心率，属于几何方法，运算量小，方便快捷．
本题还有设直线AB方程，与椭圆方程联解，寻求a、b、c的一个关系式，再解一个关于离心率的方程，但是计算过程较为繁琐，同学们不妨试试，加以比较．
解答：
解：如图，设设椭圆的左准线为l，过A点作AC⊥l于C，过点B作BD⊥l于D，再过B点作BG⊥AC于G，
直角△ABG中，∠BAG=60°，所以AB=2AG，…①
由圆锥曲线统一定义得：
，∵
∴AC=2BD
直角梯形ABDC中，AG=AC-BD=
…②①、②比较，可得AB=AC，
又∵
∴
答：所求的离心率为
点评：运用圆锥曲线的统一定义，结合解含有60°的直角三角形，求椭圆的离心率，属于几何方法，运算量小，方便快捷．
本题还有设直线AB方程，与椭圆方程联解，寻求a、b、c的一个关系式，再解一个关于离心率的方程，但是计算过程较为繁琐，同学们不妨试试，加以比较．
练习册系列答案
相关题目
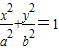的左焦点F且倾斜角为60°的直线交椭圆于A、B两点，若
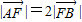，则椭圆的离心率e＝________．
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点，若
，则椭圆的离心率e= ．
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点，若
，则椭圆的离心率e= ．
|=2
，则椭圆的离心率e=__________．