题目内容
已知平面向量 满足|
满足| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为
的夹角为 ,以
,以 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
【答案】分析:以  ,
, 为邻边作平行四边形,则此平行四边形的两条对角线分别为
为邻边作平行四边形,则此平行四边形的两条对角线分别为  +
+ ,
, -
- ,分别求出他们的模,然后进行比较,即可得到结论.
,分别求出他们的模,然后进行比较,即可得到结论.
解答:解:∵ ,
, ,
, 与
与  的夹角为
的夹角为 
∴ ,
, ,
,
∴| +
+ |=
|= =
=
∴| -
- |=
|= =
=
 <
<
故以 ,
, 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 ;
;
故答案为: .
.
点评:此题是个中档题.本题考查向量的运算法则:平行四边形法则、向量的数量积的定义式以及向量的模计算公式.体现了数形结合的思想,同时也考查了学生应用知识分析解决问题的能力.
 ,
, 为邻边作平行四边形,则此平行四边形的两条对角线分别为
为邻边作平行四边形,则此平行四边形的两条对角线分别为  +
+ ,
, -
- ,分别求出他们的模,然后进行比较,即可得到结论.
,分别求出他们的模,然后进行比较,即可得到结论.解答:解:∵
 ,
, ,
, 与
与  的夹角为
的夹角为 
∴
 ,
, ,
,
∴|
 +
+ |=
|= =
=
∴|
 -
- |=
|= =
=
 <
<
故以
 ,
, 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 ;
;故答案为:
 .
.点评:此题是个中档题.本题考查向量的运算法则:平行四边形法则、向量的数量积的定义式以及向量的模计算公式.体现了数形结合的思想,同时也考查了学生应用知识分析解决问题的能力.

练习册系列答案
相关题目
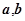 满足
满足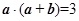 ,且
,且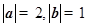 ,则向量
,则向量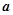 与
与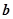 的夹角为( )
的夹角为( )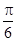 B.
B.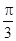 C.
C.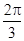 D.
D.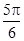
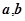 满足
满足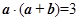 ,且
,且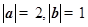 ,则向量
,则向量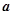 与
与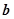 的夹角为
的夹角为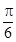 B.
B.
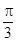 C.
C. 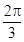 D.
D. 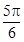
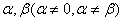 满足
满足 ,且
,且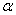 与
与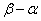 的夹角为120°,
的夹角为120°, 的取值范围是__________________ .
的取值范围是__________________ .