题目内容
设向量 =
= ,
,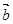 =
=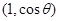 ,
,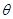 为锐角.
为锐角.
(1)若 ∥
∥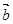 ,求tanθ的值;
,求tanθ的值;
(2)若 ·
·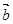 =
=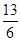 ,求sin
,求sin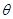 +cos
+cos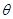 的值.
的值.
【答案】
(1)2(2)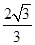
【解析】
试题分析:(1)∵ =
=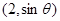 ,
,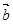 =
=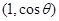 ,且
,且 ∥
∥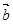 2分
2分
∴ 2 cos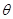 - sin
- sin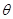 =0,∴tanθ=2.
5分
=0,∴tanθ=2.
5分
(2)因为a·b=2+sinθcosθ=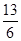 ,所以sinθcosθ=
,所以sinθcosθ=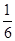 .
8分
.
8分
所以 (sinθ+cosθ)2=1+2 sinθcosθ=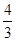 .
10分
.
10分
又因为θ为锐角,所以sinθ+cosθ=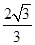 . 12分
. 12分
考点:向量的数量积,同角关系式
点评:解决的关键是利用向量的共线来得到正切值,然后结合同角关系式来求解,属于基础题。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
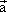 =(4sinα,-
=(4sinα,- =(-4,cosα),且
=(-4,cosα),且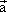 ∥
∥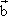 ,则锐角α为________.
,则锐角α为________. 中的三个内角分别为
中的三个内角分别为 .
. 是等腰三角形;
是等腰三角形;