题目内容
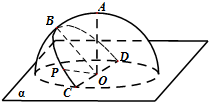 (2012•四川)如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )
(2012•四川)如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )分析:由题意求出AP的距离,然后求出∠AOP,即可求解A、P两点间的球面距离.
解答: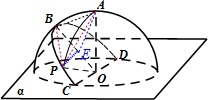 解:半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,所以CD⊥平面AOB,
解:半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,所以CD⊥平面AOB,
因为∠BOP=60°,所以△OPB为正三角形,P到BO的距离为PE=
R,E为BQ的中点,AE=
=
R,
AP=
=
R,
AP2=OP2+OA2-2OP•OAcos∠AOP,
R2=R2+R2-2R2cos∠AOP,
cos∠AOP=
,∠AOP=arccos
,
A、P两点间的球面距离为Rarccos
,
故选A.
 解:半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,所以CD⊥平面AOB,
解:半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,所以CD⊥平面AOB,因为∠BOP=60°,所以△OPB为正三角形,P到BO的距离为PE=
| ||
| 2 |
R2+(
|
|
AP=
(
|
| ||||
| 2 |
AP2=OP2+OA2-2OP•OAcos∠AOP,
8-2
| ||
| 4 |
cos∠AOP=
| ||
| 4 |
| ||
| 4 |
A、P两点间的球面距离为Rarccos
| ||
| 4 |
故选A.
点评:本题考查反三角函数的运用,球面距离及相关计算,考查计算能力以及空间想象能力.

练习册系列答案
相关题目
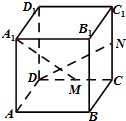 (2012•四川)如图,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成的角的大小是
(2012•四川)如图,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成的角的大小是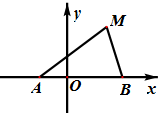 (2012•四川)如图,动点M到两定点A(-1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.
(2012•四川)如图,动点M到两定点A(-1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.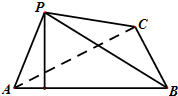 (2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上.
(2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上.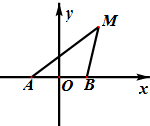 (2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.
(2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.