题目内容
设定义在（0，+∞）上的函数f（x）满足以下条件：①对于任意实数a，b，都有f=f（a）+f（b）-p，其中p是正实数；②f（2）=p-1；（2）③x＞1时，总有f（x）＜p（1）求
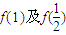的值（写成关于p的表达式）；（2）求证：f（x）在（0，+∞）上是减函数．
【答案】分析：本题考查的是抽象函数与函数的单调性知识的综合应用问题．在解答时，对于（1）只需要利用特值得方法即可获得解答；对于（2）要利用好条件③再结合单调性的定义证明即可获得解答．
解答：解：（1）∵f（a）+f（b）-P=f（a•b），
令a=b=1，则f（1）=P
=
∴
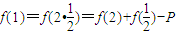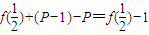
（2）设0＜x1＜x2，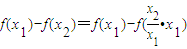
=
=
∵
，∴
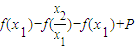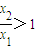∴f（x1）-f（x2）＞0，
∴f（x）在（0，+∞）上是减函数．
点评：本题考查的是抽象函数与函数的单调性知识的综合应用问题．在解答的过程当中充分体现了抽象函数特值的思想、函数单调性以及问题转化的思想．值得同学们体会反思．
解答：解：（1）∵f（a）+f（b）-P=f（a•b），
令a=b=1，则f（1）=P
=∴
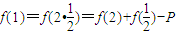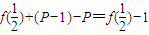
（2）设0＜x1＜x2，
=
=∵
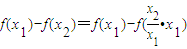
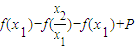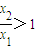，∴∴f（x1）-f（x2）＞0，∴f（x）在（0，+∞）上是减函数．
点评：本题考查的是抽象函数与函数的单调性知识的综合应用问题．在解答的过程当中充分体现了抽象函数特值的思想、函数单调性以及问题转化的思想．值得同学们体会反思．
练习册系列答案
相关题目