题目内容
设各项为正的等比数列{an}的公比q≠1,且a3,a5,a6成等差数列,则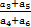 的值为( )
的值为( )
A.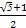 | B.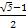 |
C. | D.2 |
B
解析

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
设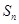 是等差数列
是等差数列 的前
的前 项和,公差
项和,公差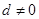 ,若
,若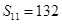 ,若
,若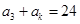 ,则正整数
,则正整数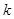 的值为( )
的值为( )
A. | B. | C. | D. |
等差数列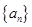 中,
中,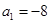 ,它的前16项的平均值是7,若从中抽取一项,余下的15项的平均值为7.2,则抽取的是()
,它的前16项的平均值是7,若从中抽取一项,余下的15项的平均值为7.2,则抽取的是()
| A.第7项 | B.第8项 | C.第15项 | D.第16项 |
在等差数列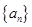 中,已知
中,已知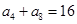 ,则该数列前11项和
,则该数列前11项和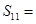 ( )
( )
| A.58 | B.88 | C.143 | D.176 |
等差数列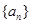 的前
的前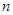 项和
项和 ,若
,若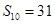 ,
,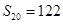 ,则
,则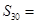 ( )
( )
| A.153 | B.182 | C.242 | D.273 |
若数列{an}是等差数列,则数列{bn}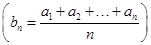 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
A.dn=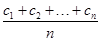 | B.dn=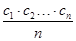 |
C.dn= 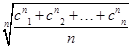 | D.dn=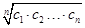 |
已知数列{an},{bn}满足a1=b1=3,an+1-an=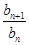 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
| A.92 012 | B.272 012 | C.92 013 | D.272 013 |
已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且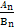 =
=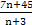 ,则使得
,则使得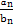 为整数的正整数n的个数是( )
为整数的正整数n的个数是( )
| A.2 | B.3 | C.4 | D.5 |
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列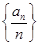 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列.其中的真命题为( ).
| A.p1,p2 | B.p3,p4 | C.p2,p3 | D.p1,p4 |