题目内容
设函数
，则对任意实数a和b，a+b＜0是f（a）+f（b）＞0的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
C
分析：先分析函数，可知函数为奇函数且为增函数，从而可判断．
解答：∵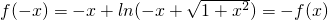
，∴函数为奇函数，又函数为增函数，所以可知对任意实数a和b，a+b＜0是f（a）+f（b）＞0的充要条件．
故选C．
点评：本题主要考查函数的性质，考查充要条件，分析性质是解题的关键．
分析：先分析函数，可知函数为奇函数且为增函数，从而可判断．
解答：∵
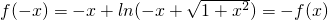，∴函数为奇函数，又函数为增函数，所以可知对任意实数a和b，a+b＜0是f（a）+f（b）＞0的充要条件．故选C．
点评：本题主要考查函数的性质，考查充要条件，分析性质是解题的关键．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
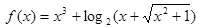，则对任意实数a、b,
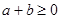是
的（ ）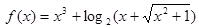
，则对任意实数a、b,
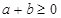是
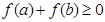的（ ）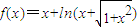
，则对任意实数a和b，a+b＜0是f（a）+f（b）＞0的（ ）
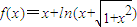，则对任意实数a和b，a+b＜0是f（a）+f（b）＞0的（ ）