题目内容
已知a、b为常数,且a≠0,函数f(x)=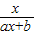 ,且f(3)=1,又方程f(x)=x有唯一解.
,且f(3)=1,又方程f(x)=x有唯一解.(I)求f(x)的解析式及方程f(x)=x的解;
(Ⅱ)当xn=f(xn-1)(n>1),数列
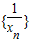 是何数列?请说明理由.
是何数列?请说明理由.
【答案】分析:(I)将方程f(x)=x进行等价变形,利用根的判别式△═0,解得b=1.再由f(3)=1,解出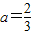 ,可得
,可得
f(x)的解析式,进而求出方程f(x)=x的解;
(II)由(I)的解析式,得xn=f(xn-1)即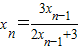 ,变形整理得
,变形整理得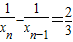 (n>1).由此可得
(n>1).由此可得
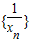 构成公差为
构成公差为 的等差数列.
的等差数列.
解答:解:(I)∵f(x)=x有唯一解,即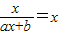 有唯一解
有唯一解
∴有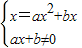 ,即
,即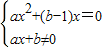
满足△=(b-1)2-4a•0=0,解之得b=1. …(2分)
又∵f(3)=1,得3=3a+1.
∴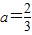 可得
可得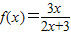 .…(3分)
.…(3分)
由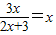 ,解得方程f(x)=x的解为x=0. …(4分)
,解得方程f(x)=x的解为x=0. …(4分)
(II)由xn=f(xn-1)(n>1),得
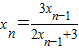 ,可得
,可得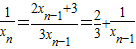 …(6分)
…(6分)
∴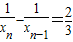 (n>1).
(n>1).
即当n>1时,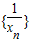 构成公差为
构成公差为 的等差数列. …(8分)
的等差数列. …(8分)
点评:本题给出分式函数,在已知f(3)=1且f(x)=x有等根的情况下求函数的解析式,并证明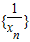 构成等差数列.着重考查了用一元二次方程根的判别式处理分式函数问题和等等差数列的通项与定义等知识,属于中档题.
构成等差数列.着重考查了用一元二次方程根的判别式处理分式函数问题和等等差数列的通项与定义等知识,属于中档题.
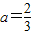 ,可得
,可得f(x)的解析式,进而求出方程f(x)=x的解;
(II)由(I)的解析式,得xn=f(xn-1)即
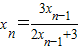 ,变形整理得
,变形整理得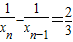 (n>1).由此可得
(n>1).由此可得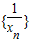 构成公差为
构成公差为 的等差数列.
的等差数列.解答:解:(I)∵f(x)=x有唯一解,即
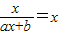 有唯一解
有唯一解∴有
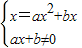 ,即
,即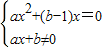
满足△=(b-1)2-4a•0=0,解之得b=1. …(2分)
又∵f(3)=1,得3=3a+1.
∴
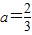 可得
可得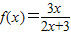 .…(3分)
.…(3分)由
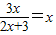 ,解得方程f(x)=x的解为x=0. …(4分)
,解得方程f(x)=x的解为x=0. …(4分)(II)由xn=f(xn-1)(n>1),得
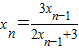 ,可得
,可得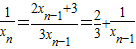 …(6分)
…(6分)∴
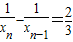 (n>1).
(n>1).即当n>1时,
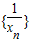 构成公差为
构成公差为 的等差数列. …(8分)
的等差数列. …(8分)点评:本题给出分式函数,在已知f(3)=1且f(x)=x有等根的情况下求函数的解析式,并证明
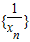 构成等差数列.着重考查了用一元二次方程根的判别式处理分式函数问题和等等差数列的通项与定义等知识,属于中档题.
构成等差数列.着重考查了用一元二次方程根的判别式处理分式函数问题和等等差数列的通项与定义等知识,属于中档题. 
练习册系列答案
相关题目