题目内容
14.已知函数g(x)=lnx-(x+1)(1)求函数g(x)的极大值;
(2)求证:ln($\frac{n+1}{n}$)<$\frac{1}{n}$(n∈N+)
分析 (1)求出g(x)的导数,求得单调区间,进而得到极大值;
(2)构造函数f(x)=ln(1+x)-x,x>0,求出导数,判断单调性,即可得证.
解答 (1)解:函数g(x)=lnx-(x+1)的导数为g′(x)=$\frac{1}{x}$-1,
当x>1时,g′(x)<0,g(x)在(1,+∞)递减;
当0<x<1时,g′(x)>0,g(x)在(0,1)递增.
即有g(x)在x=1处取得极大值,且为-2;
(2)证明:构造函数f(x)=ln(1+x)-x,x>0,
f′(x)=$\frac{1}{1+x}$-1=$\frac{-x}{1+x}$,
即有f(x)在(0,+∞)递减,
则f(x)<f(0)=0,
即为ln(1+x)<x,
令x=$\frac{1}{n}$,则有ln(1+$\frac{1}{n}$)<$\frac{1}{n}$,
故ln($\frac{n+1}{n}$)<$\frac{1}{n}$(n∈N+).
点评 本题考查导数的运用:求单调区间和极值,主要考查求极值的方法,同时考查不等式的证明,注意运用函数的单调性,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
2.已知点P($\frac{3}{2}$,-1)在抛物线E:x2=2py(p>0)的准线上,过点P作抛物线的切线,若切点A在第一象限,F是抛物线E的焦点,点M在直线AF上,点N在圆C:(x+2)2+(y+2)2=1上,则|MN|的最小值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{6}{5}$ | C. | 2 | D. | 6$\sqrt{2}$-1 |
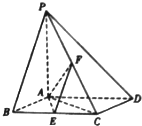 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB中点. 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.