题目内容
某班主任对班级22名学生进行了作业量多少的调查,数据如下:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
(Ⅰ)根据以上数据建立一个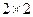 列联表;
列联表;
(Ⅱ)试问喜欢电脑游戏与认为作业多少是否有关系?
(可能用到的公式: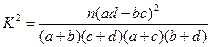 ,可能用到数据:
,可能用到数据: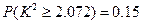 ,
,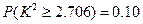 ,
, ,
, .)
.)
(1)根据题中所给数据,得到如下列联表:
(2) 认为作业多 认为作业不多 总 计 喜欢玩电脑游戏 9 3 12 不喜欢玩电脑游戏 4 6 10 总 计 13 9 22 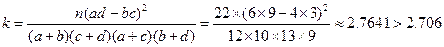
∴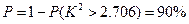
∴有90%的把握认为喜欢玩电脑游戏与认为作业多少有关.
解析

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组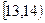 ,第二组
,第二组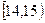 ……第五组
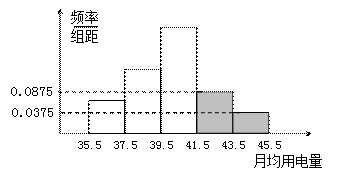
……第五组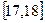 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.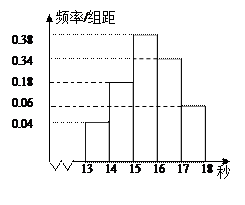
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设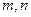 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知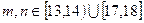
求事件“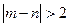 ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 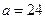 | 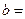 ______ ______ | _____ |
| 不达标 | 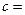 _____ _____ | 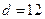 | _____ |
| 合计 | ______ | ______ | 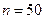 |
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
② 请问哪位技术员检验更稳定?并说明理由.
(本小 题满分12分)
题满分12分)
上海世 博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示.
| 分 组 (单位:岁) | 频数 | 频 率 |
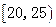 | 5 | 0.050 |
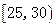 | ① | 0.200 |
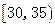 | 35 | ② |
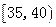 | 30 | 0.300 |
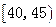 | 10 | 0.100 |
| 合 计 | 100 | 1.00 |
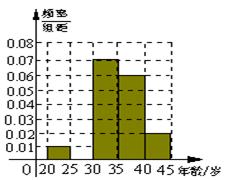
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图,
再根据频率分布直方图估计这507名画师中年龄
 在
在 岁的人数(结果取整数);
岁的人数(结果取整数);(2)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会
 深
深圳馆志愿者活动,其中选取2名
 画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为
画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为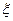 ,求
,求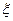 的分布列及数学期望.
的分布列及数学期望. (本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| | 感染 |  未感染 未感染 | 总计 |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
 (
( 1)求出列联表中数据
1)求出列联表中数据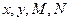 的值;
的值;(2)写出
 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式:

 参考数据:
参考数据: | 0.05 | 0.025 | 0.010 |
 | 3.841 | 5.024 | 6.635 |
(本小题满分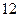 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
| | 不及格 | 及格 | 总计 |
| 甲班 | 10 | 35 | M |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | N |
(2) 写出求k
 观测值的计算式
观测值的计算式(3) 假设k
 =0.6527你有多大把握认为成绩及格与班级
=0.6527你有多大把握认为成绩及格与班级 有关?
有关?k
 =7.121又说明什么?
=7.121又说明什么?(P(k

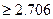 )
)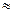 0.100,P(k
0.100,P(k
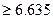 )
)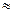 0.010)
0.010) 
 高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
高度大约是多少?(计算时可以用组中值代替各组数据的平均值); 组中移出一棵树苗,从
组中移出一棵树苗,从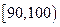 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则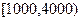 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内) 某居民月收入在
某居民月收入在 内的频率;
内的频率; (3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在
(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在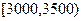 内的居民中抽取多少人?
内的居民中抽取多少人?