题目内容
(1)已知a,b是正常数,a≠b,x,y∈(0,+∞),求证: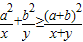 ,指出等号成立的条件;
,指出等号成立的条件;(2)利用(1)的结论求函数
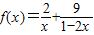 (
(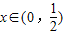 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.
【答案】分析:(1)利用基本不等式a2+b2≥2ab,乘积一定,和有最小值,等号成立的条件是两正数相等;
(2)利用(1)的结论,将(2)变形为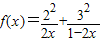 即可.
即可.
解答:解:(1)应用二元均值不等式,得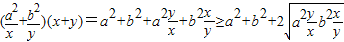 =(a+b)2,
=(a+b)2,
故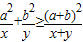 .
.
当且仅当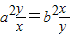 ,即
,即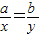 时上式取等号.
时上式取等号.
(2)由(1)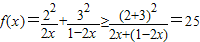 .
.
当且仅当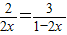 ,即
,即 时上式取最小值,即[f(x)]min=25.
时上式取最小值,即[f(x)]min=25.
点评:本题考查不等式的应用,另外给你一种解题工具,让你应用它来解答某一问题,这是近年考试命题的一种新颖的题型之一,很值得读者深刻反思和领悟当中的思维本质.
(2)利用(1)的结论,将(2)变形为
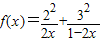 即可.
即可.解答:解:(1)应用二元均值不等式,得
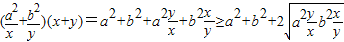 =(a+b)2,
=(a+b)2,故
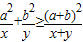 .
.当且仅当
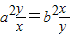 ,即
,即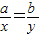 时上式取等号.
时上式取等号.(2)由(1)
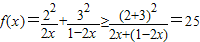 .
.当且仅当
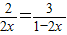 ,即
,即 时上式取最小值,即[f(x)]min=25.
时上式取最小值,即[f(x)]min=25.点评:本题考查不等式的应用,另外给你一种解题工具,让你应用它来解答某一问题,这是近年考试命题的一种新颖的题型之一,很值得读者深刻反思和领悟当中的思维本质.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
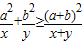 ,指出等号成立的条件;
,指出等号成立的条件;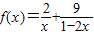 (
(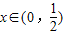 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.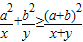 ,指出等号成立的条件;
,指出等号成立的条件;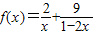 (
(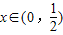 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.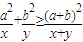 ,指出等号成立的条件;
,指出等号成立的条件;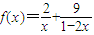 (
(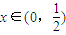 )的最小值,指出取最小值时x的值.
)的最小值,指出取最小值时x的值.