题目内容
某同学准备用反证法证明如下一个问题：函数f（x）在[0，1]上有意义，且f（0）=f（1），如果对于不同的x1，x2∈[0，1]，都有|f（x1）-f（x2）|＜|x1-x2|，求证：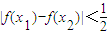
．那么他的反设应该是 ．
【答案】分析：根据反证法证明的步骤，首先反设，反设是否定原命题的结论，分析原命题的结论，可得这是一个全称命题，写出其否定，即可得答案．
解答：解：根据反证法证明的步骤，
首先反设，反设是否定原命题的结论，
故答案为“?x1，x2∈[0，1]，当|f（x1）-f（x2）|＜|x1-x2|时，有|f（x1）-f（x2）|≥
．
点评：本题考查反证法的运用，注意反设即否定原命题的结论，要结合命题的否定．
解答：解：根据反证法证明的步骤，
首先反设，反设是否定原命题的结论，
故答案为“?x1，x2∈[0，1]，当|f（x1）-f（x2）|＜|x1-x2|时，有|f（x1）-f（x2）|≥
．点评：本题考查反证法的运用，注意反设即否定原命题的结论，要结合命题的否定．
练习册系列答案
相关题目
在
上有意义,且
,如果对于不同的
,都有
，求证：
。那么他的反设应该是___________．
，那么它的假设应该是（ ）．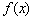
在
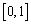上有意义,且
,如果对于不同的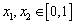
,都有
，求证：
。那么他的反设应该是___________．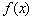
在
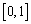上有意义,且
,如果对于不同的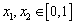
,都有
，求证：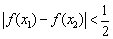
。那么他的反设应该是___________．