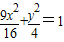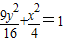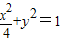题目内容
从圆O:x2+y2=4上任意一点P向x轴作垂线,垂足为P′,点M是线段PP′的中点,则点M的轨迹方程是( )
分析:由题意,可令M(x,y),由点M是线段PP'的中点可得出P(x,2y),再由P是圆O上一点,及圆O:x2+y2=4,可得x2+(2y)2=4,整理即可得到点M的轨迹方程选出正确答案
解答:解:由题意,令M(x,y),则P(x,2y),
又圆O:x2+y2=4上任意一点P
∴x2+(2y)2=4,整理得
+y2=1
故选D
又圆O:x2+y2=4上任意一点P
∴x2+(2y)2=4,整理得
| x2 |
| 4 |
故选D
点评:本题考查求轨迹问题,根据求谁设谁的规律,先设出要求的轨迹上的一点坐标,用它表示出已知轨迹方程的曲线上相应点的坐标,代入已知的轨迹方程即可求得所求的轨迹方程,解题的关键是准确理解题意,

练习册系列答案
相关题目
从圆O:x2+y2=4上任意一点P向x轴作垂线,垂足为P',点M是线段PP'的中点,则点M的轨迹方程是( )
A.
| B.
| ||||||||
C.x2+
| D.
|