题目内容
设函数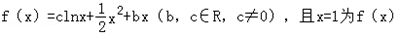 的极值点.
的极值点.
(I)若函数f(x)在x=2的切线平行于3x﹣4y+4=0,求函数f(x)的解析式;
(II)若f(x)=0恰有两解,求实数c的取值范围.
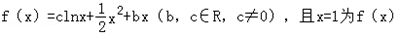 的极值点.
的极值点.(I)若函数f(x)在x=2的切线平行于3x﹣4y+4=0,求函数f(x)的解析式;
(II)若f(x)=0恰有两解,求实数c的取值范围.
解:(I)求导函数,可得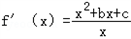
∵x=1是函数f(x)的极值点,函数f(x)在x=2的切线平行于3x﹣4y+4=0,
∴f′(1)=0,f′(2)=
∴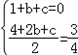
∴b=﹣ ,c=
,c= 
∴函数f(x)的解析式为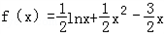 ;
;
(II)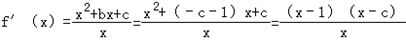 (x>0)
(x>0)
①若c<0,则f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,f(x)=0恰有两解,则f(1)<0,即
∴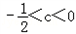
②若0<c<1,则f极大(x)=f(c)=clnc+ ,f极小(x)=f(1)=
,f极小(x)=f(1)=
∵b=﹣1﹣c,
∴f极大(x)=clnc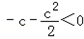 ,f极小(x)=
,f极小(x)=
∴f(x)=0不可能有两解
③若c≥1,则f极小(x)=clnc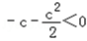 ,f极大(x)=
,f极大(x)= 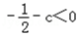 ,
,
∴f(x)=0只有一解
综上可知,实数c的取值范围为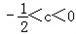
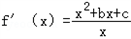
∵x=1是函数f(x)的极值点,函数f(x)在x=2的切线平行于3x﹣4y+4=0,
∴f′(1)=0,f′(2)=

∴
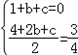
∴b=﹣
 ,c=
,c= 
∴函数f(x)的解析式为
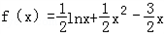 ;
;(II)
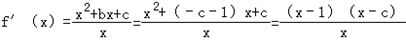 (x>0)
(x>0)①若c<0,则f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,f(x)=0恰有两解,则f(1)<0,即

∴
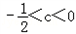
②若0<c<1,则f极大(x)=f(c)=clnc+
 ,f极小(x)=f(1)=
,f极小(x)=f(1)=
∵b=﹣1﹣c,
∴f极大(x)=clnc
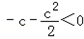 ,f极小(x)=
,f极小(x)=
∴f(x)=0不可能有两解
③若c≥1,则f极小(x)=clnc
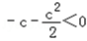 ,f极大(x)=
,f极大(x)= 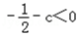 ,
,∴f(x)=0只有一解
综上可知,实数c的取值范围为
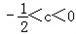

练习册系列答案
相关题目
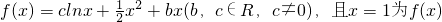 的极值点.
的极值点. 的极值点.
的极值点.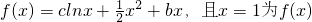 的极值点.
的极值点.