题目内容
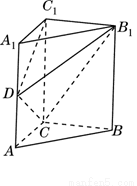
 如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.(1)求异面直线BC与AC1的夹角;
(2)求证:AC1∥平面CDB1.
分析:(1)根据异面直线所成角的定义进行求解.(2)利用线面平行的判定定理判断.
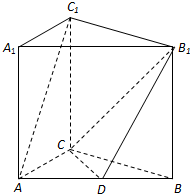
解答: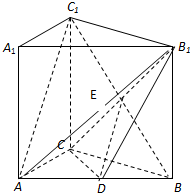 解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1
解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1
∴CB与AC1的夹角等于AC1与C1B1的夹角…2
设直三棱柱高为x,由已知可得AC1=
,C1B1=4,
AB1=
,…5
显然有AB12=C1B12+AC12.
∴AC1⊥C1B1,即CB与与AC1的夹角为90°…7
(2)连结C1B交CB1于E,再连结DE,
由已知可得E为C1B的中点,…9
又∵D为AB的中点,∴DE为△BAC1的中位线.
∴AC1∥DE…12
又∵DE?平面CDB1,AC1?平面CDB1
∴AC1∥平面CDB1…14
 解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1
解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1∴CB与AC1的夹角等于AC1与C1B1的夹角…2
设直三棱柱高为x,由已知可得AC1=
| x2+9 |
AB1=
| x2+25 |
显然有AB12=C1B12+AC12.
∴AC1⊥C1B1,即CB与与AC1的夹角为90°…7
(2)连结C1B交CB1于E,再连结DE,
由已知可得E为C1B的中点,…9
又∵D为AB的中点,∴DE为△BAC1的中位线.
∴AC1∥DE…12
又∵DE?平面CDB1,AC1?平面CDB1
∴AC1∥平面CDB1…14
点评:本题主要考查空间异面直线所成角的确定和求法,以及空间直线和平面平行的判断,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
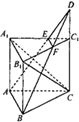 (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线. (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.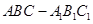 中,
中,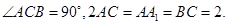
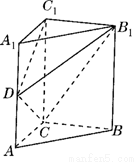
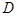 为
为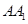 的中点,求证:平面
的中点,求证:平面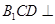 平面
平面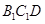 ;
;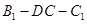 的大小为
的大小为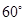 ,试确定
,试确定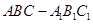 中,
中,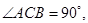
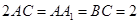 ,
,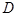 为
为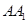 的中点
的中点
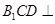 平面
平面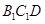 ;
;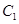 到平面
到平面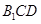 的距离.
的距离.