题目内容
在锐角 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
.
(1)求B;
(2)若 ,求
,求 .
.
(1) ;(2)4.
;(2)4.
解析试题分析:(1)首先用诱导公式把 化成
化成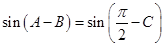 ,
,
因为 都是锐角,根据正弦函数的单调性知:
都是锐角,根据正弦函数的单调性知: ,再结合三角形内角和定理可解角
,再结合三角形内角和定理可解角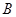 .
.
(2)由(1)的结果,在 中,已知两边和其中一边的对角,可用正弦定理或余弦定理求
中,已知两边和其中一边的对角,可用正弦定理或余弦定理求 .要注意锐角三角形条件,防止增解.
.要注意锐角三角形条件,防止增解.
试题解析:(1)由sin(A-B)=cosC,得sin(A-B)=sin( -C).
-C).
∵△ABC是锐角三角形,
∴A-B= -C,即A-B+C=
-C,即A-B+C= , ①
, ①
又A+B+C=π, ②
由②-①,得B= . 6分
. 6分
(2)由余弦定理b2=c2+a2-2cacosB,得
(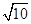 )2=c2+(3
)2=c2+(3 )2-2c×3
)2-2c×3 cos
cos ,
,
即c2-6c+8=0,解得c=2,或c=4.
当c=2时,b2+c2-a2=(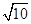 )2+22-(3
)2+22-(3 )2=-4<0,
)2=-4<0,
∴b2+c2<a2,此时A为钝角,与已知矛盾,∴c≠2.
故c=4. 12分
考点:1、诱导公式;2、正弦定理、余弦定理、解三角形.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
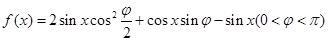 在
在 处取最小值.
处取最小值. 的值。
的值。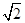 ,
,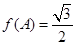 ,求角C.
,求角C. ,求△ABC的面积.
,求△ABC的面积. , sin B=3sin C.
, sin B=3sin C. ,求△ABC的面积.
,求△ABC的面积. 函数
函数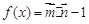 .
.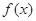 的最小正周期和对称轴的方程;
的最小正周期和对称轴的方程; 的角
的角 的对边分别为
的对边分别为 ,且
,且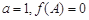 ,求
,求 的取值范围.
的取值范围.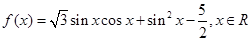 .
.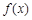 最大值和最小正周期;
最大值和最小正周期;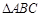 内角
内角 所对的边分别为
所对的边分别为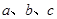 ,且
,且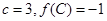 .若
.若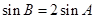 ,求
,求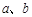 的值.
的值.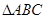 中,角
中,角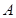 、
、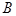 、
、 的对边分别为
的对边分别为 、
、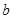 、
、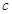 .设向量
.设向量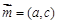 ,
,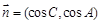 .
.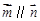 ,
,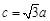 ,求角
,求角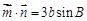 ,
, ,求
,求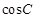 的值.
的值. 。
。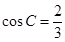 ,求
,求 的值。
的值。 中,已知
中,已知 ,求边
,求边 的长及
的长及