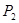题目内容
有甲、乙两个单位都愿意聘用你,而你能获得如下信息:甲单位不同职位月工资x1/元 | 1 200 | 1 400 | 1 600 | 1 800 |
获得相应职位的概率P1 | 0.4 | 0.3 | 0.2 | 0.1 |
乙单位不同职位月工资x2/元 | 1 000 | 1 400 | 1 600 | 2 200 |
获得相应职位的概率P2 | 0.4 | 0.3 | 0.2 | 0.1 |
根据工资待遇的差异情况,你愿意选择哪家单位?
解:根据月工资的分布列,计算得
Ex1=1 200×0.4+1 400×0.3+1 600×0.2+1 800×0.1=1 400,
Dx1=
(1 200-1 400)2×0.4+(1 400-1 400)2×0.3+(1 600-1 400)2×0.2+(1 800-1 400)2×0.1=40 000;
Ex2=1 000×0.4+1 400×0.3+1 800×0.2+2 200×0.1=1 400,
Dx2=(1 000-1 400)2×0.4+(1 400-1 400)2×0.3+(1 800-1 400)2×0.2+(2 200-1 400)2×0.1=112 000.
因为Ex1=Ex2,Dx1<Dx2,所以两家单位的工资均值相等,但甲单位不同职位的工资相对集中,乙单位不同职位的工资相对分散.这样,如果你希望不同职位的工资差距小一些,就选择甲单位;如果你希望不同职位的工资差距大一些,就选择乙单位.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案招聘会上,某公司决定先试用后再聘用小强,该公司的甲、乙两个部门各有4个不同岗位.
(Ⅰ)公司随机安排小强在这两个部门中的3个岗位上进行试用,求小强试用的3个岗位中恰有2个在甲部门的概率;
(Ⅱ)经试用,甲、乙两个部门都愿意聘用他.据估计,小强可能获得的岗位月工资及相应概率如下表所示:
|
甲部门不同岗位月工资 |
2200 |
2400 |
2600 |
2800 |
|
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
|
乙部门不同岗位月工资 |
2000 |
2400 |
2800 |
3200 |
|
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
求甲、乙两部门月岗位工资的期望与方差,据此请帮助小强选择一个部门,并说明理由.
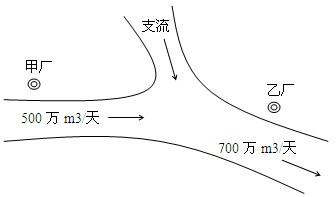 如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.
如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.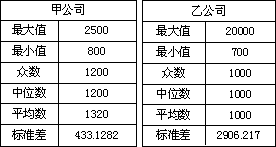
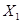 (元)
(元)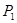
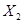 (元)
(元)