题目内容
已知函数
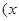 >
>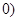 ,其中r为有理数,且0<r<1. 则
,其中r为有理数,且0<r<1. 则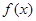 的最小值为_______;
的最小值为_______;
0
解析试题分析:因为函数
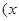 >
> ,其中r为有理数,且0<r<1.所以
,其中r为有理数,且0<r<1.所以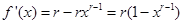 ,由于0<r<1,故可知当f’(x)>0,得到x=1,可知当x>1,导数大于零,函数递增,当0<x<1,,导数小于零,函数递减,故可知当x=1时函数取得最小值为0.故答案为0.
,由于0<r<1,故可知当f’(x)>0,得到x=1,可知当x>1,导数大于零,函数递增,当0<x<1,,导数小于零,函数递减,故可知当x=1时函数取得最小值为0.故答案为0.
考点:本题主要是考查导数在究函数中的运用。
点评:解决该试题的关键是先求解函数的导数,然后根据导数的正负与函数单调性的关系来求解函数的最值。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 .,其中a,b∈R
.,其中a,b∈R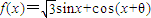 的定义域为R,最大值为1(其中θ为常数,且
的定义域为R,最大值为1(其中θ为常数,且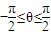 ).
).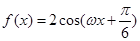 ,(其中
,(其中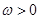 ,x∈R)的最小正周期为
,x∈R)的最小正周期为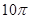 .
. ,
,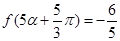 ,
,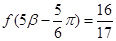 ,求
,求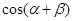 的值.
的值.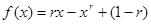
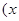 >
>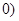 ,其中r为有理数,且0<r<1. 则
,其中r为有理数,且0<r<1. 则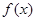 的最小值为_______;
的最小值为_______;