题目内容
设
是互不垂直的两条异面直线，则下列命题成立的是（ ）
A．存在唯一直线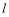
，使得
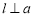，且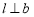
B．存在唯一直线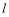，使得
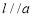，且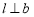
C．存在唯一平面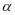
，使得
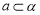，且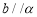
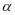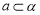D．存在唯一平面，使得，且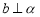
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
设是互不垂直的两条异面直线，则下列命题成立的是（ ）
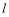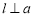A．存在唯一直线，使得，且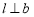
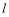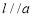B．存在唯一直线，使得，且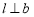
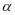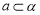C．存在唯一平面，使得，且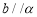
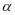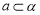D．存在唯一平面，使得，且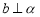
天天向上一本好卷系列答案小学生10分钟应用题系列答案
的图象大致是（ ）
满足
，当
时，
，若在
上，方程
有三个不同的实根，则实数
的取值范围是（ ）
B．
D．
的顶上有一高度为
的建筑物
，为了测量该山坡相对于水平地面的坡角
，在山坡的
处测得
，沿山坡前进
到达
处，又测得
，根据以上数据计算可得
B．
D．
是函数
的一个极值点．
；
的单调区间；
与函数
的图象有3个交点，求
的取值范围．
的家庭大约有___________户．
是定义在
上的奇函数，当时
，
.
的解析式；
.
中，
，点
是
的中点，将
沿
折起到
的位置，使二面角
是直二面角.
；
的余弦值.